Вы здесь
4.4. Определение динамики состояния пострадавшего при смертельных травматических субдуральных гематомах
Одним из вопросов, важным в правовом отношении и сложным для экспертного решения, является определение динамики клинического состояния пострадавшего и возможности совершать целенаправленные действия при НЧМТ с наличием СГ. В настоящее время в клиническом течении СГ выделяют 5 следующих фаз: компенсации, субкомпенсации, умеренной декомпенсации, грубой декомпенсации и терминальную фазу [31,37]. В аспекте рассматриваемого вопроса целесообразно объединение первых трех фаз в так называемый «светлый промежуток», в течение которого пострадавший сохраняет способность к совершению целенаправленных действий, а последние две фазы можно обозначить как интегральный терминальный промежуток, в течение которого пострадавший в силу тяжести своего состояния лишен такой возможности [66].
Важной особенностью клинического течения СГ является выраженная зависимость сроков клинической манифестации сдавления ГМ и развития его дислокации от множества факторов, основными из которых являются наличие иной внутричерепной травматической патологии, объем и локализация СГ [31,37,38]. Поэтому для травматических СГ, ассоциированных с ОПГМ, характерным считается отсутствие светлого промежутка, а для изолированных СГ – наличие такового. Однако в практике нередкими бывают случаи сохранения сознания даже при наличии ОПГМ [494]. В качестве возможного объяснения отсутствия нарушений сознания в подобных ситуациях рассматривались многие факторы, в том числе и неточное установление причин смерти потерпевших [495]. При наличии же светлого промежутка в динамике клинического состояния пострадавших с наличием травматических СГ продолжительность первого может случайным образом варьировать от нескольких часов до нескольких суток, недель и даже месяцев [97,496,497].
В некоторых случаях для юридической оценки событий, связанных с причинением травматической СГ, требуется определение наличия и продолжительности не светлого, а интегрального терминального промежутка в динамике церебральной компрессии. Например, Р. Leth и А. Vesterby описали наблюдение убийства 61-летнего мужчины путем его повешения после предварительного избиения с последующей инсценировкой самоубийства [498]. При исследовании трупа потерпевшего была обнаружена объемная СГ с выраженным отеком ГМ. Это позволило сделать экспертный вывод об отсутствии сознания у потерпевшего и, соответственно, отсутствии у него способности к совершению активных действий во время процедуры повешения, прижизненность которого была доказана благодаря обнаружению кровоизлияний в коже из области странгуляционной борозды [498].
Однако экспертные методики объективного определения наличия и длительности светлого и интегрального терминального промежутков при травматических СГ, приведших к смерти в условиях неочевидности, до последнего времени фактически отсутствовали. Вместе с тем автором была выявлена зависимость сроков формирования вторичных ВСК и инфарктов мозга от продолжительности сдавления ГМ и предложены соответствующие хронологические модели развития церебральной дислокации. Данное обстоятельство делает принципиально возможным установление длительности интегрального терминального промежутка при смертельных СГ.
Изложенное определило необходимость дальнейшего изучения выявленных закономерностей, а также поиск других критериев, оценка которых наряду с данными о наличии вторичных ВСК и инфарктов мозга могла бы применяться для объективного определения динамики состояния пострадавшего, его возможности совершать целенаправленные действия при травматических СГ, приведших к смерти в условиях неочевидности.
В этой связи автором было ретроспективно изучено 405 наблюдений летальной НЧМТ с наличием супратенториальных СГ, сопровождавшихся сдавлением ГМ, у 333 (78,8%) лиц мужского и 72 (21,2%) лиц женского пола в возрасте 14-93 лет, с известными обстоятельствами и давностью причинения.
Проведенное исследование подтвердило выраженное влияние на частоту светлого промежутка такого фактора, как ассоциация СГ с другой внутричерепной травматической патологией. Так, при изолированных супратенториальных СГ отмечалось более частое наличие светлого промежутка, чем при их ассоциации с СК (р
Таблица 26 Точечные и интервальные оценки частот светлого промежутка при различных видах НЧМТ с наличием супратенториальных СГ
| Вид НЧМТ | n | 95% нижняя | Точечная | 95% верхняя |
| СГ без СК и ОПГМ | 25 | 0,688 | 0,880 | 0,975 |
| СГ с СК без ОПГМ | 71 | 0,306 | 0,423 | 0,546 |
| СГ с ОПГМ | 309 | 0,134 | 0,175 | 0,222 |
Сравнение продолжительности светлого промежутка в анализируемых выборках НЧМТ, также доказало значимую межгрупповую неоднородность этого показателя (χ2 = 71,055; ν = 2; p = 0,00001). При этом рассматриваемые клинико-анатомические формы НЧМТ в порядке убывания длительности светлого промежутка формировали следующую последовательность: изолированные СГ, ассоциации СГ с СК, ассоциации СГ с ОПГМ (табл. 27).
Корреляционный анализ не выявил значимой зависимости продолжительности светлого промежутка при смертельной НЧМТ с наличием супратенториальных СГ от таких факторов, как суммарный объем гематомы (r = -0,031; t = -0,582; p = 0,561) и возраст пострадавшего (r = 0,095; t = 1,918; p = 0,056). 95% двусторонние интервальные оценки для неизвестных коэффициентов ρ указанных статистических зависимостей составили соответственно
-0,136≤ ρ <0,074,
-0,002≤ ρ <0,191.
Однако асимметричность приведенных ДИ относительно нуля свидетельствовала о наличии слабой отрицательной зависимости продолжительности светлого промежутка от суммарного объема СГ и слабой положительной его зависимости от возраста пострадавшего.
Изложенные результаты указывали на целесообразность дальнейшего изучения длительности светлого промежутка лишь для выделенных клинико-анатомических вариантов НЧМТ.
Анализ рассматриваемых выборок НЧМТ показал, что все указанные распределения продолжительности светлого промежутка являются унимодальными с выраженной положительной асимметрией, причем мода каждого из них равна нулю. Более резко правосторонняя асимметрия была присуща распределениям длительности светлого промежутка для супратенториальных СГ, ассоциированных с СК и ОПГМ.
Таблица 27 Выборочные оценки распределений продолжительности светлого промежутка при НЧМТ с наличием супратенториальных СГ, ч
| Характер СГ | n | \[\bar x\] | \[\tilde x\] | s | xmin | xmax | |
| Изолированные | 25 | 878,0 | 93 | 3464,0 | 0 | 17424 | |
| Ассоциации СГ с СК* | ≥ 0 | 71 | 35,8 | 0 | 107,0 | 0 | 539 |
| > 0 | 30 | 84,8 | 4 | 152,7 | 0,5 | 539 | |
| Ассоциации СГ с ОПГМ* | ≥ 0 | 309 | 13,7 | 0 | 54,2 | 0 | 487 |
| > 0 | 54 | 78,2 | 28,5 | 109,1 | 0,7 | 487 | |
Примечание. * - для указанных выборок дополнительно приведены оценки распределений совокупностей только положительных значений продолжительности светлого промежутка.
Ввиду характерности отсутствия светлого промежутка в клиническом течении указанных вариантов НЧМТ медианы распределений длительности данного показателя также равнялись нулю (см. табл. 27). Вследствие этого ни одно из анализируемых распределений не могло быть описано каким-либо типом из множества известных теоретических распределений с хорошо изученными статистическими свойствами. В этой связи интервальные оценки указанных распределений рассчитывались на основе неравенства Чебышева [48,50,59]. Поскольку нижние интервальные оценки данных распределений заведомо равны нулю, определению подлежали лишь односторонние верхние интервальные оценки (табл. 28).
Синтез полученных результатов делает возможным указание в практической судебно-медицинской экспертной деятельности для каждой из выделенных клинико-анатомических вариантов НЧМТ следующих оценок наличия и длительности светлого промежутка:
- вероятности наличия или отсутствия;
- медианы длительности (типичного значения);
- выборочного среднего длительности;
- ДИ длительности с любой требуемой степенью доверия.
Следует отметить, что применение неравенства Чебышева позволяет получать только слишком широкие ДИ продолжительности светлого промежутка. Использование таких ДИ можно считать необходимым только при оценке изолированных СГ, реально характеризующихся большой величиной размаха возможных значений длительности светлого промежутка. В остальных случаях разработанные на основе неравенства Чебышева ДИ будут малопригодными для практики. В этой связи дополнительному статистическому анализу были подвергнуты выборки с положительными значениями светлого промежутка.
Рассмотрение дополнительных выборок показало, что соответствующие плотности вероятностей могут быть достаточно точно аппроксимированы семейством логнормальных распределений с параметрами μ = 2,32382057 и σ = 2,28922764 для супратенториальных СГ, сочетанных с СК (рис. 86), и μ = 3,34068787 и σ = 1,60318480 для аналогичных СГ, ассоциированных с ОПГМ (рис. 87).
Таблица 28 Верхние интервальные оценки продолжительности светлого промежутка при НЧМТ с наличием супратенториальных СГ, ч и сутки
| Вариант НЧМТ | \[\bar x + s/\sqrt \alpha \] | ||||
| 1 - α | 0,8 | 0,9 | 0,95 | 0,99 | 0,999 |
| Изолированные СГ | 8623,8 | 11832,2 | 16369,6 | 35518,3 | 110420,1 |
| 359,33 | 493,01 | 682,07 | 1479,93 | 4600,84 | |
| Ассоциации СГ с СК | 275,0 | 374,1 | 514,2 | 1105,4 | 3418,1 |
| 11,46 | 15,59 | 21,42 | 46,06 | 142,42 | |
| Ассоциации СГ с ОПГМ | 134,8 | 185,0 | 256,0 | 555,4 | 1726,9 |
| 5,62 | 7,71 | 10,67 | 23,14 | 71,95 | |
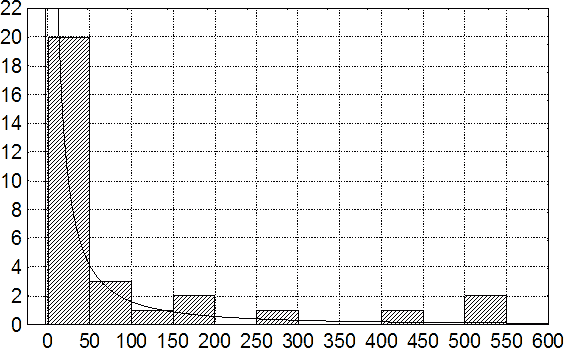
Рис. 86. Гистограмма положительных значений длительности светлого промежутка в динамике супратенториальных СГ, ассоциированных с СК. Здесь и на рис. 87 по оси абсцисс – длительность светлого промежутка, ч; по оси ординат – количество наблюдений. Линиями показаны аппроксимирующие функции плотностей вероятностей семейства логнормальных распределений.
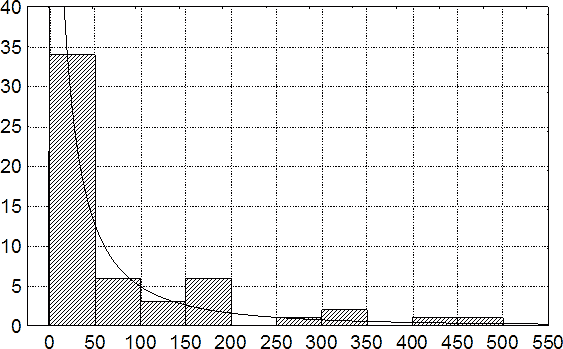
Рис. 87. Гистограмма положительных значений длительности светлого промежутка в динамике супратенториальных СГ, ассоциированных с ОПГМ.
Знание параметров μ и σ функций плотностей распределений вероятностей позволяет вычислять следующие оценки длительности светлого промежутка в динамике выделенных вариантов НЧМТ с наличием супратенториальных СГ:
1) вероятность соответствия неизвестной истинной длительности t светлого промежутка любому значению на промежутке от х1 до х2:
\[P({x_1} \lt t \le {x_2}) = \frac{1}{{\sigma \sqrt {2\pi } }}\int\limits_{{x_1}}^{{x_2}} {\exp \left\{ { - \frac{{{{(\ln t - \mu )}^2}}}{{2{\sigma ^2}}}} \right\}dt;\left( 1 \right)} \]
2) вероятность превышения t определенного значения x:
\[P(x \le t) = \frac{1}{{\sigma \sqrt {2\pi } }}\int\limits_x^{ + \infty } {\exp \left\{ { - \frac{{{{(\ln t - \mu )}^2}}}{{2{\sigma ^2}}}} \right\}dt;(2)} \]
3) вероятность того, что t не превысит заданное значение x:
\[P(t \le x) = \frac{1}{{\sigma \sqrt {2\pi } }}\int\limits_0^x {\exp \left\{ { - \frac{{{{(\ln t - \mu )}^2}}}{{2{\sigma ^2}}}} \right\}dt} ;(3)\]
4) математическое ожидание и медиану длины светлого промежутка:
\[M(x) = {e^{\left( {\mu + \frac{1}{2}{\sigma ^2}} \right)}};(4)\]
\[{\rm{Me}} = {e^\mu };(5)\]
5) односторонние верхние интервальные оценки длительности светлого промежутка для любой требуемой степени доверительной вероятности (табл. 29).
Применительно к выражениям (1-5) логически обоснованной является следующая базовая конструкция экспертных выводов относительно способности пострадавшего к совершению осознанных действий при НЧМТ с наличием супратенториальных СГ: «С вероятностью потерпевший сразу после причинения ему данной формы НЧМТ обладал (не обладал) способностью к совершению осознанных действий. При условии обладания потерпевшим этой способностью ее средняя длительность составляет – M(x), типичная - Ме, максимальная – xmax, а минимальная - xmin со статистической надежностью 1 – α».
Таблица 29 Оценки длительности светлого промежутка для аппроксимирующих функций плотностей распределений вероятностей, ч
| Вариант НЧМТ | 1 - α | Ме | M(x) | ||||
| 0,8 | 0,9 | 0,95 | 0,99 | ||||
| Ассоциации СГ с СК | max | 70,1 | 192,0 | 441,1 | 2099,3 | 10,21 | 140,34 |
| min | 1,49 | 0,54 | 0,24 | 0,05 | |||
| Ассоциации СГ с ОПГМ | max | 108,8 | 220,4 | 394,5 | 1176,4 | 28,24 | 102,08 |
| min | 7,33 | 3,62 | 2,02 | 0,68 | |||
При реконструкции динамики клинического течения НЧМТ с наличием супратенториальных СГ помимо характеристики светлого, важным также является установление длительности интегрального терминального промежутка. В соответствии с хронологической моделью сроков формирования вторичных ВСК при сдавлении ГМ супратенториальными СГ терминальный интегральный промежуток при отсутствии ВСК равняется периоду t1, а при наличии вторичных ВСК - периоду t1 + t2. Причем M(t2)=M(t1+t2)-M(t1)=27,7 ч.
Отсюда определение длительности интегрального терминального промежутка при смертельных травматических СГ осуществлялось с учетом наличия или отсутствия вторичных ВСК. Анализ хронологии интегрального терминального промежутка проводился при условии отсутствия проведения пострадавшим трепанации черепа, в том числе и диагностического характера.
Анализ соответственно 58 и 138 наблюдений церебральной компрессии показал, что плотность вероятностей продолжительности интегрального терминального промежутка наиболее адекватно аппроксимируется семейством логнормальных распределений с параметрами μ = 1,26588420 и σ = 0,925434282 при отсутствии вторичных ВСК, а также μ = 2,75689797 и σ = 1,27667583 при их наличии (рис. 88,89).
Знание параметров μ и σ функций плотностей распределений вероятностей позволяет в отношении интегрального терминального промежутка по формулам (1-5) вычислять оценки, аналогичные таковым для светлого промежутка.
Например, вероятность того, что длительность интегрального терминального промежутка у пострадавших с супратенториальными СГ, погибших от дислокации ГМ при отсутствии вторичных ВСК, составит 10 ч или более равна
\[P(10 \le t) = \frac{1}{{0,925434282 \cdot \sqrt {2\pi } }}\int\limits_{10}^{ + \infty } {\exp \left\{ { - \frac{{{{(\ln t - 1,26588420)}^2}}}{{2 \cdot {{0,925434282}^2}}}} \right\}dt} = 0,131\]
Соответственно вероятность длительности интегрального терминального промежутка у данной группы пострадавших не более 10 ч составляет P(t<10)=1-0,131=0,869.
Вычисленные значения вероятностей P(10 ≤t) и P(<10) тождественны значениям долей наблюдений травматического сдавления ГМ, в которых длительность интегрального терминального промежутка при отсутствии вторичных ВСК составляет не менее или не более 10 ч соответственно.
Математическое ожидание, медиана и односторонние интервальные оценки длительности интегрального терминального промежутка при дислокации ГМ без развития и с развитием вторичных ВСК для наиболее важных уровней вероятности приведены в таблице 30.
Таблица 30 Оценки длительности интегрального терминального промежутка при различных исходах церебральной дислокации для аппроксимирующих функций плотностей вероятностей, ч
| Исход дислокации ГМ | 1 - α | Ме | M(x) | ||||
| 0,8 | 0,9 | 0,95 | 0,99 | ||||
| Отсутствие ВСК | max | 7,7 | 11,6 | 16,2 | 30,5 | 3,55 | 5,44 |
| min | 1,63 | 1,08 | 0,77 | 0,41 | |||
| Вторичные ВСК | max | 46,1 | 80,9 | 128,6 | 307,0 | 15,75 | 35,58 |
| min | 5,37 | 3,07 | 1,93 | 0,81 | |||
| Инфаркты ГМ | max | 343,3 | 514,1 | 717,6 | 1341,3 | 158,63 | 241,57 |
| min | 73,24 | 48,91 | 35,04 | 18,75 | |||
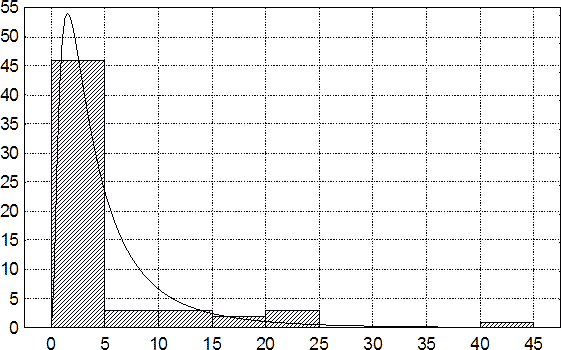
Рис. 88. Гистограмма продолжительности интегрального терминального промежутка при летальной НЧМТ с наличием супратенториальных СГ и отсутствием вторичных ВСК. Здесь и на рис. 89,90 по оси абсцисс – длительность интегрального терминального промежутка, ч; по оси ординат – количество наблюдений. Линиями показаны аппроксимирующие функции плотностей распределения вероятностей.
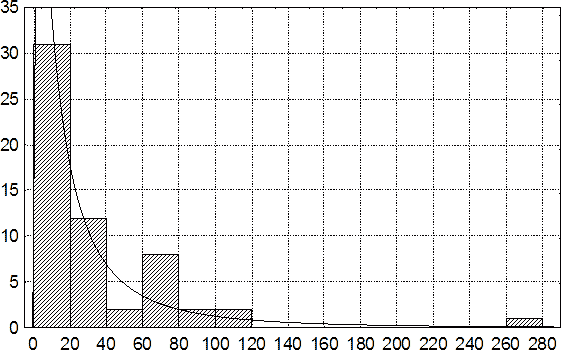
Рис. 89. Гистограмма длительности интегрального терминального промежутка при летальной НЧМТ с наличием супратенториальных СГ и вторичных ВСК.
В отличие от летального исхода сдавления ГМ с отсутствием вторичных ВСК для судебно-медицинской практики при дислокациях ГМ с развитием указанных кровоизлияний актуальным является определение не верхних, а нижних односторонних интервальных оценок ее длительности. Например, при 97,5% уровне надежности минимальная длительность интегрального терминального промежутка у пострадавших с супратенториальными СГ, погибших от дислокации ГМ с развитием вторичных ВСК, составляет 1,3 ч.
Помимо вторичных ВСК определение длительности интегрального терминального промежутка при дислокациях ГМ, вызванных СГ, возможно также по наличию церебральных инфарктов. Из двух типов инфарктов, характерных для церебральных дислокаций при супратенториальных СГ, актуальными в судебно-медицинском отношении являются только инфаркты, развивающиеся в бассейнах задних мозговых артерий. В отличие от вторичных ВСК инфаркты указанного типа не являются обязательным исходом пролонгированной церебральной компрессии. Отсюда для установления длительности интегрального терминального промежутка значение имеет только факт развития инфарктов данного типа.
Анализ 16 наблюдений НЧМТ с наличием супратенториальных СГ, осложнившихся развитием инфарктов в бассейнах задних мозговых артерий, показал, что аппроксимация плотности вероятностей длительности интегрального терминального промежутка для данного варианта церебральной дислокации может быть вполне адекватно осуществлена логнормальным распределением с параметрами формы и масштаба μ = 5,06618995 и σ = 0,917844116 (рис. 90). Знание указанных параметров позволяет в случаях развития инфарктов в бассейнах задних мозговых артерий по формулам (1-5) вычислять такой же набор оценок длительности интегрального терминального промежутка, какой актуален при церебральных дислокациях с развитием вторичных ВСК (см. табл. 30).
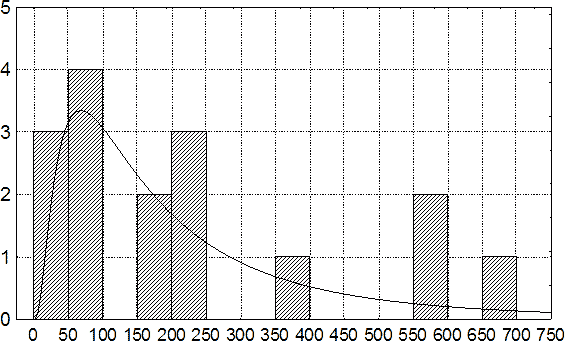
Рис. 90. Гистограмма продолжительности интегрального терминального промежутка при летальной НЧМТ с наличием супратенториальных СГ, осложнившихся формированием инфарктов мозга в бассейнах задних мозговых артерий.
Приведенные данные актуальны не только в аспекте определения динамики клинического состояния пострадавшего, но и в плане идентификации давности НЧМТ с наличием СГ.
Из двух составляющих длительности НЧМТ с наличием СГ наибольший интерес представляет интегральный терминальный промежуток, поскольку последний менее вариабелен и его развитие при смертельных церебральных дислокациях обязательно. При этом можно утверждать, что давность летальной НЧМТ с наличием СГ составляет не менее продолжительности терминального промежутка.
В практическом отношении при установлении давности НЧМТ по длительности интегрального терминального промежутка важным является выявление таких осложнений дислокации мозга, как вторичные ВСК и его инфаркты с последующим определением одного из возможных 4 типов дислокации ГМ:
- с отсутствием вторичных ВСК и инфарктов мозга;
- с наличием вторичных ВСК и отсутствием инфарктов;
- с наличием инфарктов мозга и отсутствием вторичных ВСК;
- с наличием и вторичных ВСК, и инфарктов мозга.
После этого для конкретного типа церебральной дислокации аналитически по формулам (1-5) или с помощью табулированных данных (см. табл. 29,30) с требуемой статистической надежностью устанавливается длительность интегрального терминального промежутка и, соответственно, нижняя грань давности НЧМТ.

