Вы здесь
3.2. Количественная морфологическая диагностика давности инкапсулированных и резорбированных субдуральных гематом
Ввиду отсутствия хорошо воспроизводимых и доступных для практической реализации решений по-прежнему актуальной остается проблема морфометрической диагностики давности СГ. Поскольку регистрация различных гистометрических и гистостереометрических показателей практически возможна только применительно к инкапсулированным и резорбированным СГ, то в действительности изложенная задача морфометрической диагностики сводится лишь к установлению давности СГ указанных морфологических типов.
В этой связи автором было выполнено слепое проспективное исследование, целью которого явилась разработка воспроизводимых и нетрудоемких способов морфометрического определения давности инкапсулированных и резорбированных СГ.
Объектами проведенного исследования явились фрагменты капсул и содержимого 55 инкапсулированных СГ и фрагменты ТМО в проекции 39 резорбированных СГ, взятые от трупов лиц с наличием открытой или закрытой НЧМТ, погибших в возрасте 24-90 лет в различные сроки посттравматического периода длительностью от 8 суток до 2,5 лет. В каждом случае забирали 1-3 фрагмента ТМО и капсул СГ. Забранный материал фиксировали в нейтральном растворе формалина и заливали в парафин. Изготовленные гистологические срезы окрашивали гематоксилином и эозином.
Выбор подлежащих морфометрическому исследованию показателей определялся необходимостью их устойчивости к усадке тканей под воздействием процедуры приготовления гистологических срезов. Поэтому регистрировали гистостереометрические и относительные счетные показатели. Наряду с ними исследовался также один абсолютный линейный гистометрический признак с небольшой степенью подверженности влиянию усадки тканей – показатель толщины капсулы СГ. Для уменьшения трудоемкости гистометрии в качестве данного показателя была выбрана максимальная толщина капсулы, оценивание которой требует осуществления небольшой серии измерений. В итоге в качестве потенциальных морфометрических критериев давности СГ рассматривались и подвергались слепому оцениванию 8 количественных показателей их капсул:
- относительный объем клеточных элементов;
- относительный объем сосудов;
- доля макрофагов в клеточном инфильтрате;
- доля лимфоцитов и плазмоцитов в клеточном инфильтрате;
- доля нейтрофилов в клеточном инфильтрате;
- доля фибробластов в клеточном инфильтрате;
- относительный объем гемосидероза;
- максимальная толщина.
Морфометрическое исследование проводили с использованием микроскопа MICROS серии MC 300 TX. Максимальную толщину капсул СГ оценивали с помощью винтового окулярного микрометра МОВ-1-15x, предварительно калиброванного по объект-микрометру проходящего света ОМП. Капсулу СГ фотографировали по всем полям зрения с помощью цифровой фотокамеры NICON COOLPIX 8400 под увеличениями 26x, 64x, 129x, 258x и 644x. Гистостереометрические и относительные счетные признаки определяли по цифровым микрофотографиям путем их сплошного сканирования с помощью инструментов «Счетчик» и «Сетка» программы Adobe Photoshop CS3 Extended версии 10.0.1.
Визуальный анализ полученных морфометрических данных показал, что эволюция капсул СГ характеризуется умеренными или слабыми монотонными отрицательными зависимостями относительных объемов клеточного и сосудистого компонентов, долей всех популяций воспалительного генеза в клеточном инфильтрате и аналогичной силы монотонными положительными зависимостями доли фибробластов в клеточном инфильтрате, относительного объема гемосидероза и толщины капсулы от давности НЧМТ (рис. 46-53). Аналитически указанные стохастические зависимости могут быть представлены следующими аппроксимациями:
\[{V_C} = 0,307 - 0,0418\ln t,\]
\[{V_V} = 0,0814 - 4,9794 \cdot {10^{ - 5}}t,\]
\[{V_H} = 0,0139 - 0,0035\ln t,\]
\[{N_M} = 0,1576 - 0,0002t,\]
\[{N_L} = 0,0834 - 0,0071\ln t,\]
\[{N_N} = 0,0702 - 0,0075\ln t,\]
\[{N_F} = 0,6477 - 0,0344\ln t,\]
\[l = 126,1559 + 83,1878\ln t,\]
где V – относительный объем; N – доля в клеточном инфильтрате; подстрочные индексы С, V, H, M, L, N, F – принадлежность показателя к характеристикам клеточного и сосудистого компонентов, гемосидероза, макрофагов, лимфоплазмоцитарных клеток, нейтрофилов и фибробластов соответственно; l – максимальная толщина капсулы, мкм, t – давность НЧМТ, сутки.
Приведенные логарифмические функции формально определяемы на множестве всех положительных чисел, а линейные аппроксимации – на множестве всех действительных чисел. Однако хронологические промежутки, в области которых указанные функции имеют физический смысл, включают только определенные подмножества положительных чисел. Так, функция NM(t) имеет физический смысл на промежутке \[t \in [7;7 \cdot {10^2}]\] суток. Остальные приведенные функции имеют физический смысл на временном отрезке \[t \in [10;9 \cdot {10^2}]\] суток.
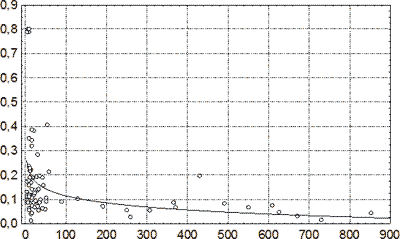
Рис. 46. Зависимость относительного объема клеточных элементов в капсулах СГ от длительности посттравматического периода. По оси абсцисс – давность НЧМТ, сутки; по оси ординат – относительный объем клеточных элементов. Линией показана аппроксимация выборочных данных логарифмической регрессией.
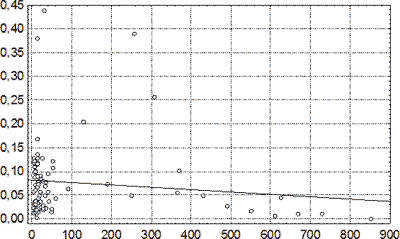
Рис. 47. Зависимость относительного объема сосудов в капсулах СГ от длительности посттравматического периода. По оси абсцисс – давность НЧМТ, сутки; по оси ординат – относительный объем сосудов. Линией показана аппроксимация выборочных данных линейной регрессией.
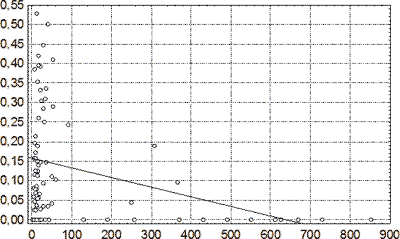
Рис. 48. Зависимость доли макрофагов в клеточном инфильтрате капсул СГ от длительности посттравматического периода. По оси абсцисс – давность НЧМТ, сутки; по оси ординат – доля макрофагов. Линией показана аппроксимация выборочных данных линейной регрессией.
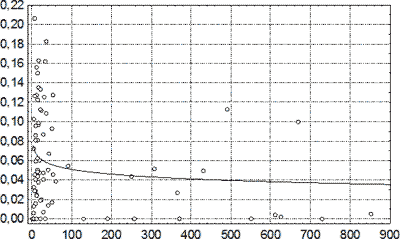
Рис. 49. Зависимость доли лимфоцитов и плазмоцитов в клеточном инфильтрате капсул СГ от длины посттравматического периода. По оси абсцисс – давность НЧМТ, сутки; по оси ординат – доля лимфоидных клеток. Линией показана аппроксимация выборочных данных логарифмической регрессией.
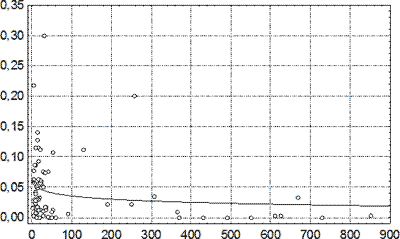
Рис. 50. Зависимость доли нейтрофилов в клеточном инфильтрате капсул СГ от длительности посттравматического периода. По оси абсцисс – давность НЧМТ, сутки; по оси ординат – доля нейтрофилов. Линией показана аппроксимация выборочных данных логарифмической регрессией.
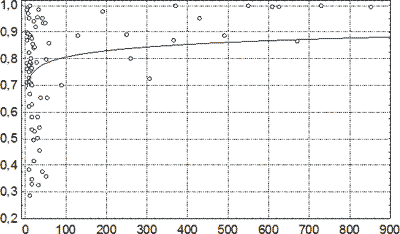
Рис. 51. Зависимость доли фибробластов в клеточном инфильтрате капсул СГ от длительности посттравматического периода. По оси абсцисс – давность НЧМТ, сутки; по оси ординат – доля фибробластов. Линией показана аппроксимация выборочных данных логарифмической регрессией.
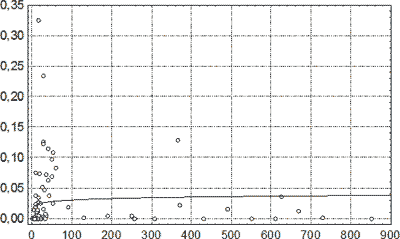
Рис. 52. Зависимость относительного объема скоплений гемосидерина в капсулах СГ от длительности посттравматического периода. По оси абсцисс – давность НЧМТ, сутки; по оси ординат – относительный объем гемосидероза. Линией показана аппроксимация выборочных данных логарифмической регрессией.
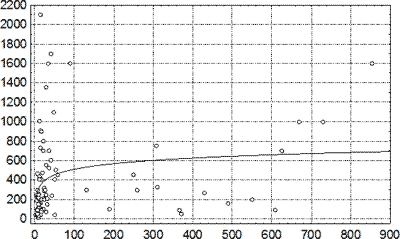
Рис. 53. Зависимость максимальной толщины капсулы СГ от длительности посттравматического периода. По оси абсцисс – давность НЧМТ, сутки; по оси ординат – максимальная толщина капсулы, мкм. Линией показана аппроксимация выборочных данных логарифмической регрессией.
Статистические характеристики анализируемых зависимостей компонентов капсул СГ от давности НЧМТ приведены в таблице 16. Из таблицы видно, что зависимости VV(t) и VH(t) при не являются статистически значимыми. Помимо t-статистики отсутствие значимости указанных стохастических зависимостей при уровне доказывает также принадлежность нуля 95% ДИ для ρ. Однако смещение названных ДИ в сторону отрицательных значений подтверждает выводы визуального анализа диаграмм рассеяния о наличии, направлении и силе зависимостей VV(t) и VH(t).
Корреляционный анализ показал, что эволюция капсул СГ характеризуется лишь умеренными или слабыми зависимостями всех исследовавшихся морфометрических показателей от давности НЧМТ (см. табл. 16). Причем указанные зависимости отличались неоднородностью остаточной дисперсии, особенно резко выраженной в начале посттравматического периода (см. рис. 46-53). Данное обстоятельство могло быть вызвано возмущающим влиянием таких факторов, как наличие выбросов и/или кластеринга.
Латентный кластеринг анализируемых показателей был обнаружен с помощью корреляционно-регрессионного анализа. А именно, наличие кластеринга было обусловлено объединением двух различных кластеров: инкапсулированных и резорбированных СГ. Феномен кластеринга исследовавшихся данных хорошо демонстрирует диаграмма рассеяния, приведенная на рисунке 54. На диаграмме видно, что кластеры инкапсулированных и резорбированных СГ отличаются регрессионными зависимостями максимальной толщины капсулы от давности НЧМТ. В частности, инкапсулированным СГ присущ большой угол наклона линии регрессии, в то время как резорбированные СГ характеризуются незначительным, статистически незначимым увеличением толщины капсулы.
Таблица 16 Характеристики стохастических зависимостей структурных компонентов капсул СГ от давности НЧМТ
| Вид связи | n | r | t | p | 95% ДИ | |||
| ρ | ρ 2 | |||||||
| \[{V_C}\left( t \right)\] | 86 | -0,258 | -2,466 | 0,017 | -0,048 | -0,433 | 0,002 | 0,197 |
| \[{V_V}\left( t \right)\] | 81 | -0,126 | -1,129 | 0,262 | -0,333 | 0,095 | 0 | 0,111 |
| \[{N_M}\left( t \right)\] | 78 | -0,339 | -3,144 | 0,002 | -0,520 | -0,125 | 0,016 | 0,270 |
| \[{N_L}\left( t \right)\] | 78 | -0,262 | -2,364 | 0,021 | -0,455 | -0,041 | 0,002 | 0,207 |
| \[{N_N}\left( t \right)\] | 78 | -0,236 | -2,121 | 0,037 | -0,014 | -0,433 | 0,0002 | 0,188 |
| \[{N_F}\left( t \right)\] | 78 | 0,378 | 3,564 | 0,001 | 0,168 | 0,551 | 0,028 | 0,304 |
| \[{V_H}\left( t \right)\] | 90 | -0,063 | -0,595 | 0,553 | -0,265 | 0,145 | 0 | 0,070 |
| \[l\left( t \right)\] | 91 | 0,213 | 2,053 | 0,043 | 0,007 | 0,400 | 0,0001 | 0,160 |
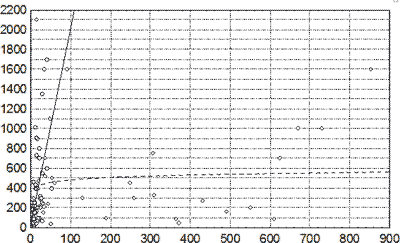
Рис. 54. Диаграмма рассеяния максимальной толщины капсулы СГ. По оси абсцисс – давность НЧМТ, сутки; по оси ординат – максимальная толщина, мкм. Знаком «кружок» обозначены инкапсулированные, знаком «ромбик» - резорбированные СГ. Сплошной линией показана аппроксимация данных линейной, пунктирной линией - логарифмической регрессиями.
Данное обстоятельство означает, что инкапсулированные СГ отличаются быстрым увеличением толщины капсулы за счет превращения свернувшейся части гематомы в грануляционную ткань. Резорбированные же СГ характеризуются относительной стабильностью данного показателя ввиду отсутствия жидкофазного компонента гематомы, который после своего свертывания представляет собой потенциальный источник увеличения толщины капсулы. Именно по причине отсутствия разделения эмпирических выборок на кластеры нерезорбированных и резорбированных СГ предпринимавшиеся ранее попытки прогнозирования давности инкапсулированных СГ по толщине их капсул оказались малоэффективными [381]. Аналогичный феномен был присущ остальным морфометрическим показателям, корреляционные зависимости которых иногда отличались не только своей силой, но и направлением (табл. 17).
После исключения кластеринга только показатели относительной доли макрофагов в клеточном инфильтрате капсулы, относительного объема гемосидероза и максимальной толщины капсулы характеризовались наличием статистически значимой зависимости от давности НЧМТ. Причем лишь первому из перечисленных показателей было присуще наличие указанной зависимости в обоих кластерах СГ. Зависимости остальных обладали статистической значимостью только внутри кластера инкапсулированных СГ (см. табл. 17).
Таблица 17 Характеристики зависимостей структурных компонентов капсул СГ различных морфологических типов от давности НЧМТ
| Вид связи | Инкапсулированные | Резорбированные | \[{p_{{\rho _1} = {\rho _2}}}\] | ||||||
| n1 | r1 | t1 | p1 | n2 | r2 | t2 | p2 | ||
| \[{V_C}\left( t \right)\] | 50 | -0,251 | -1,797 | 0,079 | 36 | -0,377 | -2,376 | 0,023 | 0,537 |
| \[{V_V}\left( t \right)\] | 45 | 0,002 | 0,013 | 0,989 | 36 | -0,217 | -1,300 | 0,202 | 0,339 |
| \[{N_M}\left( t \right)\] | 44 | 0,464 | 3,399 | 0,001 | 34 | -0,449 | -2,840 | 0,008 | 3*10-1 |
| \[{N_L}\left( t \right)\] | 44 | 0,168 | 1,106 | 0,275 | 34 | -0,294 | -1,737 | 0,092 | 0,047 |
| \[{N_N}\left( t \right)\] | 44 | 0,045 | 0,293 | 0,771 | 34 | -0,226 | -1,314 | 0,198 | 0,248 |
| \[{N_F}\left( t \right)\] | 44 | 0,045 | 0,293 | 0,771 | 34 | -0,226 | -1,314 | 0,198 | 0,248 |
| \[{V_H}\left( t \right)\] | 53 | 0,443 | 3,527 | 0,001 | 37 | -0,135 | -0,804 | 0,427 | 0,006 |
| \[l\left( t \right)\] | 53 | 0,544 | 4,628 | 3*10-5 | 38 | 0,200 | 1,225 | 0,228 | 0,065 |
Таким образом, принципиально возможными оказались следующие методы идентификации давности СГ:
- определение давности инкапсулированных СГ по показателю максимальной толщины их капсулы;
- определение давности инкапсулированных СГ по показателю относительного объема интракапсулярного гемосидероза;
- определение давности инкапсулированных СГ по показателю относительной доли макрофагов в клеточном инфильтрате капсулы;
- определение давности инкапсулированных СГ по комплексу морфометрических показателей капсулы, включающему максимальную толщину, относительный объем гемосидероза и относительную долю макрофагов в клеточном инфильтрате;
- определение давности резорбированных СГ по показателю относительной доли макрофагов в клеточном инфильтрате их капсулы.
Важно отметить, что для судебно-медицинской практики наибольший интерес представляют методы определения давности неинкапсулированных и инкапсулированных СГ, которые могут вызвать клинически значимое сдавление мозга и по этой причине являться объектом экспертного изучения. Задача установления давности резорбированных СГ возникает гораздо реже, поскольку последние представляют собой благоприятный исход эволюции гематомы.
Наибольшей выраженностью статистической зависимости от давности НЧМТ из комплекса перспективных в отношении идентификации последней морфометрических параметров обладал показатель максимальной толщины капсулы инкапсулированных СГ.
Из комплекса альтернативных регрессий наиболее адекватной задаче определения давности инкапсулированных СГ по толщине ее капсулы оказалась кубическая полиномиальная модель
\[T = 5,970 + 0,061l - 8,094 \cdot {10^{ - 5}}{l^2} + 3,382 \cdot {10^{ - 8}}{l^3} \pm 8,844{t_{\alpha ;49}}\sqrt {1 + L_0^TL{L_0}} , (1)\]
где Т – давность СГ, сутки; l – максимальная толщина капсулы СГ, мкм; ta;49 – значение t-критерия при требуемом уровне значимости α и указанном количестве степеней свободы; L0 – вектор-столбец вида
\[{L_0} = \left( {\begin{array}{*{20}{c}}1\\l\\{{l^2}}\\{{l^3}}\end{array}} \right) ;\]
\[L_0^T = \left( {\begin{array}{*{20}{c}}1&l&{{l^2}}&{{l^3}}\end{array}} \right)\]
- транспонированный вектор L0; L – матрица
\[L = \left( {\begin{array}{*{20}{c}}{1,0356453 \cdot {{10}^{ - 1}}}&{ - 6,6541811 \cdot {{10}^{ - 4}}}&{9,5467797 \cdot {{10}^{ - 7}}}&{ - 3,6032694 \cdot {{10}^{ - 10}}}\\{ - 6,6541811 \cdot {{10}^{ - 4}}}&{6,0185700 \cdot {{10}^{ - 6}}}&{ - 9,6787350 \cdot {{10}^{ - 9}}}&{3,8490015 \cdot {{10}^{ - 12}}}\\{9,5467797 \cdot {{10}^{ - 7}}}&{ - 9,6787350 \cdot {{10}^{ - 9}}}&{1,7041272 \cdot {{10}^{ - 11}}}&{ - 7,1118810 \cdot {{10}^{ - 15}}}\\{ - 3,6032694 \cdot {{10}^{ - 10}}}&{3,8490015 \cdot {{10}^{ - 12}}}&{ - 7,1118810 \cdot {{10}^{ - 15}}}&{3,0597690 \cdot {{10}^{ - 18}}}\end{array}} \right) .\]
Геометрическая интерпретация (1) представлена на рисунке 55.
Кубический полином (1), являясь статистически значимым, (F=9,184; p=6,294*10-15), обладал хорошими точечными оценками коэффициентов множественной корреляции (r = 0,600) и множественной детерминации (r2 = 0,360; скорректированный r2 = 0,321), а также относительно небольшой остаточной дисперсией (\[\left( {{s_\varepsilon } = 8,844} \right) суток.\] Каждый регрессионный коэффициент модели (1) также являлся статистически значимым
\[{\rm{(}}\left| t \right| > {\rm{2}}{\rm{,186;}}p < 0,034) .\]
Проведенное тестирование неоднородности дисперсии остатков модели (1) не обнаружило (F=0,858; p=0,626). Значение коэффициента множественной корреляции (r2=0,360) означает, что доля вариации значений давности СГ, объясняемая регрессией (1), равна 36,0%, составляя 54,2% от ее максимально возможной величины (73,6% от максимально возможного r).
Приведенные результаты определяют целесообразность использования регрессионной модели (1) в целях определения давности инкапсулированных СГ. Изложенное демонстрируют следующие примеры из судебно-медицинской экспертной практики.
Пример 1.
Максимальная толщина капсулы нерезорбированной травматической СГ, обнаруженной при судебно-медицинском исследовании трупа, равна 120 мкм. Необходимо определить точечную, а также 95% верхнюю интервальную оценки давности СГ.
Значение одностороннего t-критерия при и степенях свободы равно 1,677. Согласно регрессионной модели (1) давность СГ составляет
\[T = 12,2 \pm 15,0\]
суток.
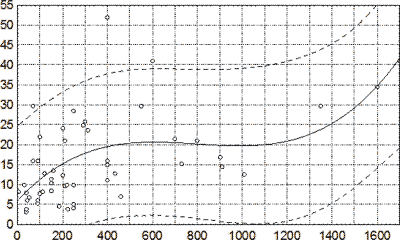
Рис. 55. Кубическая полиномиальная регрессионная модель идентификации давности инкапсулированных СГ по толщине ее капсулы. По оси абсцисс – максимальная толщина капсулы, мкм; по оси ординат – давность СГ, сутки. Знаком ○ маркированы выборочные данные, сплошной линией – кривая регрессии, пунктирными линиями – 95% ДИ для значений давности.
Таким образом, давность инкапсулированной СГ с толщиной капсулы до 120 мкм в среднем равняется 12,2 суток и с 95% статистической надежностью не превышает 27,2 суток. Истинная давность данной инкапсулированной СГ равнялась 12,9 суток. Отклонение прогнозного значения давности СГ от ее истинного значения составило 0,7 суток.
Пример 2.
Максимальная толщина капсулы нерезорбированной СГ равна 1600 мкм. Необходимо определить точечную и 90% интервальные оценки давности СГ.
Значение двустороннего t-критерия при и степенях свободы равно 1,677. Согласно регрессионной модели (1) давность СГ составляет
\[T = 34,7 \pm 15,0\] суток.
Таким образом, давность инкапсулированной СГ с толщиной капсулы до 1600 мкм в среднем равняется 34,7 суток, а 90% ДИ давности составляет 19,7-49,7 суток. Истинная давность данной инкапсулированной СГ равнялась 34,5 суткам. Отклонение прогнозного значения давности СГ от ее истинного значения составило 0,2 суток.
В отличие от своего прототипа [381] разработанный способ снижает трудоемкость определения толщины капсулы СГ путем замены точечной оценки ее математического ожидания, регистрация которого требует проведения большой серии замеров, на оценку ее максимума.
Вторым по величине модуля силы статистической зависимости от давности НЧМТ являлся показатель относительной доли макрофагов в клеточном инфильтрате капсулы инкапсулированных СГ. Наиболее адекватной задаче идентификации давности СГ по относительной доле макрофагов оказалась однофакторная линейная регрессионная модель
\[T = 10,507 + 34,171{N_M} \pm 10,098{t_{\alpha ;42}}\sqrt {1,023 + \frac{{{{({N_M} - 0,171)}^2}}}{{0,023}}} , (2)\]
где NM – относительная доля макрофагов в клеточном инфильтрате капсулы СГ.
Геометрическая интерпретация (2) представлена на рисунке 56.
Линейная регрессионная модель (2) являлась статистически значимой (F=11,551; p=0,001), по сравнению с моделью (2) характеризовалась меньшим коэффициентом корреляции и большей остаточной дисперсией
\[{s_\varepsilon } = 10,098\]
суток. Проведенное тестирование неоднородности дисперсии остатков регрессионной модели (2) не обнаружило
\[(F = 1,039;p = 0,472) .\]
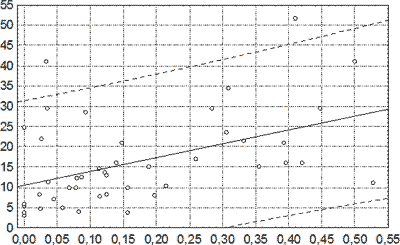
Рис. 56. Линейная регрессионная модель идентификации давности инкапсулированных СГ по относительной доле макрофагов в клеточном инфильтрате капсулы гематомы. По оси абсцисс – относительная доля макрофагов; по оси ординат – давность СГ, сутки. Знаком ○ маркированы выборочные данные, сплошной линией – прямая регрессии, пунктирными линиями – 95% ДИ для значений давности.
Доля вариации значений давности инкапсулированных СГ, объясняемая регрессией (2), равнялась 21,6%, составляя 28,4% от ее максимально возможной величины. Несмотря на небольшую долю объясняемой дисперсии, соответствующее тестирование неадекватности модели (2) не выявило
\[(F = 1,258;p = 0,327) .\]
Практическое использование показателя относительной доли макрофагов в клеточном инфильтрате капсулы СГ в целях определения ее давности может быть показано на следующих примерах.
Пример 3.
Относительная доля макрофагов в клеточном инфильтрате капсулы нерезорбированной травматической СГ, обнаруженной при судебно-медицинском исследовании трупа, равна 0,113. Необходимо определить точечную, а также 95% верхнюю интервальную оценки давности СГ.
Значение одностороннего t-критерия при и степенях свободы равно 1,682. Согласно регрессионной модели (2) давность СГ составляет T=14,4±17,2 суток.
Таким образом, давность инкапсулированной СГ с относительной долей макрофагов в клеточном инфильтрате капсулы NM=0,113 в среднем равняется 14,4 суток и с 95% статистической надежностью не превышает 31,6 суток. Истинная давность данной инкапсулированной СГ равнялась 14,6 суток. Отклонение прогнозного значения давности СГ от ее истинного значения составило 0,2 суток.
Пример 4.
Относительная доля макрофагов в клеточном инфильтрате капсулы нерезорбированной СГ равна 0,393. Необходимо определить точечную и 95% интервальные оценки давности СГ.
Значение двустороннего t-критерия при и степенях свободы равно 2,018. Согласно регрессионной модели (2) давность СГ составляет T=23,9±21,1 суток.
Таким образом, давность инкапсулированной СГ с относительной долей макрофагов в клеточном инфильтрате капсулы NM=0,393 в среднем равняется 23,9 суток и с 95% статистической надежностью находится в пределах 2,8-45,0 суток. Истинная давность данной инкапсулированной СГ равнялась 21,0 суток. Отклонение прогнозного значения давности инкапсулированной СГ от ее истинного значения составило -2,9 суток.
Последним из трехэлементного множества актуальных в плане определения давности инкапсулированных СГ являлся показатель относительного объема гемосидероза капсулы гематомы. При визуальном анализе диаграммы рассеяния выяснилось, что совокупность выборочных данных на отрезке значений относительного объема гемосидероза от 0 до 0,20 может быть аппроксимирована монотонной возрастающей регрессией. На интервале значений предиктора более 0,20 имелись выбросы, придававшие регрессии ∩ - характер (рис. 57).
На отрезке значений предиктора 0-0,20 наиболее адекватной моделью идентификации давности инкапсулированных СГ явилась однофакторная линейная регрессия
\[T = 11,262 + 212,630{V_H} \pm 8,135{t_{\alpha ;49}}\sqrt {1,020 + \frac{{{{({V_H} - 0,018)}^2}}}{{0,057}}} , (3)\]
где VH – относительный объем гемосидероза капсулы СГ.
Линейная регрессионная модель (3) являлась статистически значимой \[(F = 38,609;p = 1,096 \cdot {10^{ - 7}})\] и из множества альтернативных аппроксимаций характеризовалась наибольшим коэффициентом корреляции (r=0,664) и наименьшей остаточной дисперсией sε=8,135 суток). Проведенная проверка гетероскедастичности модели (3) не обнаружило (F=1,516; p=0,253). Доля вариации значений давности СГ, объясняемая регрессией (3), равнялась 44,1%, составляя 68,1% от ее максимально возможной величины.
Возможности применения показателя относительного объема гемосидероза для установления давности инкапсулированных СГ демонстрируют следующие практические примеры.
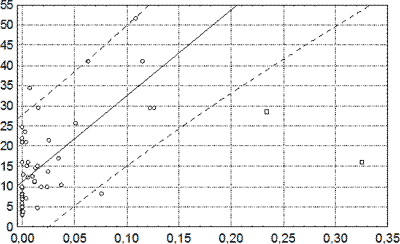
Рис. 57. Линейная регрессионная модель идентификации давности СГ по относительному объему гемосидероза ее капсулы. По оси абсцисс – относительный объем гемосидероза; по оси ординат – давность СГ, сутки. Знаком «кружок» маркированы выборочные данные, знаком «квадратик» – выбросы; сплошной линией – регрессионная линия, пунктирными линиями – 95% ДИ для значений давности.
Пример 5.
Относительный объем гемосидероза капсулы нерезорбированной травматической СГ, обнаруженной при судебно-медицинском исследовании трупа, равен 0,013. Необходимо определить точечную, а также 95% верхнюю интервальную оценки давности СГ.
Значение одностороннего t-критерия при и степенях свободы равно 1,677. Согласно регрессионной модели (3) давность СГ составляет T=14,0±13,8 суток.
Таким образом, давность инкапсулированной СГ соотносительным объемом гемосидероза VH=0,013 в среднем равняется 14,0 суток и с 95% статистической надежностью не превышает 27,8 суток. Истинная давность данной инкапсулированной СГ равнялась 14,6 суток. Отклонение прогнозного значения давности СГ от ее истинного значения составило 0,6 суток.
Пример 6.
Относительный объем гемосидероза капсулы нерезорбированной травматической СГ равен 0,051. Необходимо определить точечную и 95% интервальные оценки давности СГ.
Значение двустороннего t-критерия при и степенях свободы равно 2,010. Согласно регрессионной модели (3) давность СГ составляет T=22,1±16,7 суток.
Таким образом, давность инкапсулированной СГ соотносительным объемом гемосидероза VH=0,051 в среднем равняется 22,1 суток и с 95% статистической надежностью находится в пределах 5,5-38,8 суток. Истинная давность данной инкапсулированной СГ равнялась 25,7 суток. Отклонение прогнозного значения давности СГ от ее истинного значения составило 3,6 суток.
Относительно небольшая точность регрессионных моделей, основанных только на каком-либо одном морфометрическом показателе, определила необходимость создания многофакторной морфолого-математической модели идентификации давности инкапсулированных СГ. Анализ однофакторных и полиномиальных регрессий определил следующее множество возможных независимых переменных, адекватность вхождения которых в многофакторную регрессионную модель должна быть проверена:
\[\left\{ {l,{l^2},{l^3},{N_M},{V_H}} \right\}.\]
Пошаговый регрессионный анализ с исключением установил, что наиболее адекватной задаче определения давности инкапсулированных СГ является многофакторная регрессионная модель
\[T = 5,748 + 0,012l + 154,452{V_H} + 14,487{N_M} \pm 7,015{t_{\alpha ;40}}\sqrt {1 + X_0^TX{X_0}} , (4)\]
где Х0 – вектор-столбец, определяемый как
\[{X_0} = \left( {\begin{array}{*{20}{c}}1\\l\\{{V_H}}\\{{N_M}}\end{array}} \right) ;\]
\[X_0^T = \left( {\begin{array}{*{20}{c}}1&l&{{V_H}}&{{N_M}}\end{array}} \right)\] - транспонированный вектор Х0 (вектор-столбец); Х – квадратная матрица вида
\[X = \left( {\begin{array}{*{20}{c}}{0,0661336}&{ - 0,0000427}&{ - 0,0403735}&{ - 0,1482700}\\{ - 0,0000427}&{0,0000001}&{ - 0,0001410}&{ - 0,00000687}\\{ - 0,0403735}&{ - 0,0001410}&{24,0949025}&{ - 2,4874750}\\{ - 0,1482700}&{ - 0,00000687}&{ - 2,4874750}&{1,36893117}\end{array}} \right) .\]
Трехфакторная модель (4) являлась статистически высоко значимой \[{\rm{(}}F = {\rm{23}}{\rm{,298;}}p = 1,002 \cdot {10^{ - 8}})\] и характеризовалась наибольшими оценками коэффициентов множественной корреляции (r = 0,805) и детерминации (r2 = 0,648; скорректированный r2 = 0,620), а также наименьшей остаточной дисперсией (sε=7,015 суток). Проведенное по каждой независимой переменной тестирование неоднородности дисперсии остатков модели (4) не обнаружило (F0,134). Доля вариации значений давности СГ, объясняемая регрессией (4), равнялась 64,8%.
Указанные данные свидетельствуют о приоритетности использования регрессионной модели (4) в целях определения давности инкапсулированных СГ. Процедуру практической реализации регрессионной модели (4) демонстрирует следующий пример.
Пример 7.
При судебно-медицинском исследовании капсулы нерезорбированной травматической СГ зарегистрирован следующий вектор начальных условий: мкм, VH=0,006882, NM=0,308824. Необходимо определить точечную и 95% интервальные оценки давности СГ.
Значение двустороннего t-критерия при и степенях свободы равно 2,021. Согласно регрессионной модели (4) давность СГ составляет T=30,1±15,9 суток.
Таким образом, давность инкапсулированной СГ с указанными значениями количественных показателей в среднем равняется 30,1 суток, а 95% ДИ давности составляет 14,2-46,0 суток. Истинная давность данной инкапсулированной СГ равнялась 34,5 суткам. Отклонение прогнозного значения давности СГ от ее истинного значения составило 4,3 суток. Интересно, что в данном случае ошибка многофакторной модели превысила ошибку кубического полинома, основанного только на показателе толщины капсулы СГ (ср. с результатом примера 2).
Основной недостаток трехфакторной модели (4) связан с вхождением в нее показателя относительной доли макрофагов в клеточном инфильтрате капсулы СГ. В частности, данное вхождение ограничивало область определения функции (4) промежутком значений данного показателя от 0 до 0,20. Также регрессионный коэффициент показателя NM модели (4) не являлся статистически значимым (t=1,765; p=0,086), в отличие от остальных ее регрессионных коэффициентов (t>4,401; p
Изложенное свидетельствовало о необходимости разработки альтернативной двухфакторной модели идентификации давности СГ, в качестве независимых переменных включавшей лишь показатели максимальной толщины и относительного объема гемосидероза капсулы гематомы.
Исключение из модели (4) показателя NM привело к получению двухфакторного регрессионного уравнения
\[T = 8,693 + 0,014l + 66,145{V_H} \pm 8,691{t_{\alpha ;41}}\sqrt {1 + X_0^TX{X_0}} , (5)\]
где Х0 – вектор-столбец, определяемый как
\[{X_0} = \left( {\begin{array}{*{20}{c}}1\\l\\{{V_H}}\end{array}} \right) ;\]
\[X_0^T = \left( {\begin{array}{*{20}{c}}1&l&{{V_H}}\end{array}} \right)\] - транспонированный вектор Х0 (вектор-столбец); Х – квадратная матрица вида
\[X = \left( {\begin{array}{*{20}{c}}{0,0483009}&{ - 0,0000522}&{ - 0,1583889}\\{ - 0,0000522}&{0,0000001}&{ - 0,0000537}\\{ - 0,1583889}&{ - 0,0000537}&{5,4484025}\end{array}} \right) .\]
Двухфакторная модель (5) сохранила высокую статистическую значимость
\[{\rm{(}}F = {\rm{1}}5,{\rm{644;}}p = 8,939 \cdot {10^{ - 6}}).\]
Исключение показателя NM сопровождалось умеренным уменьшением точечных оценок коэффициентов множественной корреляции (r = 0,658) и множественной детерминации (r2 = 0,433; скорректированный r2 = 0,405), а также синхронным увеличением остаточной дисперсии (sε=8,691 суток). Проведенное по каждой независимой переменной тестирование неоднородности дисперсии остатков регрессионной модели (5) не обнаружило (F0,152). Все регрессионные коэффициенты модели (5) являлись статистически значимыми (t>3,260; p
Для демонстрации практического использования двухфакторной модели (5) продолжим рассмотрение примера 7, исключив из него показатель NM.
Пример 8.
При судебно-медицинском исследовании капсулы нерезорбированной травматической СГ зарегистрирован следующий вектор начальных условий: мкм, VH=0,006882. Необходимо определить точечную и 95% интервальные оценки давности СГ.
Значение двустороннего t-критерия при и степенях свободы равно 2,020. Согласно регрессионной модели (5) давность СГ составляет T=31,6±19,5 суток.
Таким образом, согласно регрессионной модели (5) давность инкапсулированной СГ с толщиной капсулы до 1600 мкм и относительным объемом гемосидероза VH=0,006882 в среднем равняется 31,6 суток, а 95% ДИ давности составляет 12,1-51,1 суток. Напомним, что истинная давность данной инкапсулированной СГ равнялась 34,5 суткам. Отсюда отклонение прогнозного значения давности СГ от ее истинного значения составило 2,9 суток.
На заключительном этапе исследовалась возможность разработки способа идентификации давности резорбированных СГ на основе показателя относительной доли макрофагов в клеточном инфильтрате капсулы гематомы. Регрессионный анализ в данном случае затруднялся наличием выраженной неоднородности дисперсии давности СГ при различных значениях независимой переменной (рис. 58). Указанная неоднородность проявлялась наличием большой дисперсии давности резорбированных СГ при значениях относительной доли макрофагов, близких к нулю. По мере же увеличения доли макрофагов в клеточном инфильтрате дисперсия давности резорбированных СГ значительно уменьшалась.
Некорригируемая неоднородность остаточной дисперсии допускала аналитическое определение по данному показателю лишь точечных оценок давности резорбированных СГ, не позволяя вычислять ее интервальные оценки:
\[T = 141,0776{e^{ - 6,0984{N_m}}} .(6)\]
Нелинейная по параметрам экспоненциальная модель (6) являлась статистически значимой (F=7,581; p=0,010). Доля вариации значений давности СГ, объясняемая регрессией (6), равнялась 19,2% (r = 0,438; r2 = 0,192). Остаточная дисперсия модели (6) составила 1,399. Однако данный важнейший показатель качества регрессионных уравнений ввиду существенной нелинейности экспоненциальной регрессии (6) отражал значения натурального логарифма давности СГ и вследствие этого был несопоставим с показателями остаточной дисперсии линейных или линейных по параметрам регрессионных моделей (1-5).
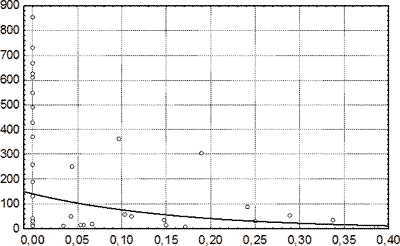
Рис. 58. Экспоненциальная регрессионная модель идентификации давности резорбированных СГ по относительной доле макрофагов в клеточном инфильтрате капсулы гематомы. По оси абсцисс – относительная доля макрофагов; по оси ординат – давность СГ, сутки. Знаком ○ маркированы выборочные данные.
Таким образом, комплекс регрессионных уравнений (1-5) позволяет аналитически с контролируемой точностью и статистической надежностью идентифицировать давность инкапсулированных СГ. Также возможным является аналитическое определение точечных оценок давности резорбированных СГ.
Важно, что модели (1,4,5), включающие в качестве одной из независимых переменных показатель максимальной толщины капсулы СГ, пригодны для идентификации давности последних только при условии приготовления гистологических срезов методом парафиновой проводки. Регрессионные модели (2,3,6), включающие в свой состав только относительные морфометрические показатели, могут быть использованы при любых методах приготовления гистологических срезов (замораживание, любые способы проводки) независимо от вида, температурного режима и сроков фиксации аутопсийного материала.
Дальнейшее увеличение точности морфометрической идентификации давности инкапсулированных и резорбированных СГ может быть достигнуто аналогично качественной гистологической диагностике путем изучения и внедрения в судебно-медицинскую экспертную практику гистохимических и иммуногистохимических методик. Также потенциально информативным остается обоснованная и воспроизводимая стратификация множества СГ с дальнейшим построением отдельных внутрикластерных регрессий.
Читать далее раздел "3.3. Определение давности субдуральных гематом по концентрации метгемоглобина"⇒

