Вы здесь
1.4. Математическое описание качественной кинетики биологических процессов в аспекте определения их давности
Разработка объективных технологий определения давности физиологических, патоморфологических или постмортальных процессов является одним из приоритетных научных направлений в судебной медицине [60]. Методология решения этой проблемы основывается на данных о стадийности изменчивости исследуемого биологического процесса и сводится к качественному выявлению и количественному оцениванию различных его проявлений.
В настоящее время общепризнанным считается, что количественные методы идентификации давности каких-либо биологических процессов потенциально наиболее информативны [61,62]. Стандартным подходом к решению проблемы определения давности биологических процессов, сопровождающихся измеряемыми изменениями, является использование методов прикладного регрессионного анализа [44,59].
Однако до сих пор значительная часть вопросов судебно-медицинского определения давности биологических процессов по-прежнему решается только путем качественного оценивания их различных проявлений. При этом полученные данные справедливо расцениваются лишь как приблизительные и имеют небольшое доказательное значение [60,62]. Вместе с тем, не следует забывать, что качественная оценка кинетики любых биологических процессов по сравнению с количественными методами исследования чаще всего отличается гораздо меньшей трудоемкостью. Кроме того, ориентировочный характер результатов качественных исследований во многом объясняется отсутствием теоретического осмысления сущности изучаемых явлений в строгой математической форме. Отсюда перспективным и необходимым методом изучения качественной кинетики любых биологических процессов представляется математическое описание их хронологии, которое позволит объективно оценивать их давность и использовать полученные оценки для решения соответствующих экспертных задач.
В этой связи в настоящем разделе излагаются разработанные автором принципы математического описания качественной кинетики различных биологических процессов и последующего объективного определения давности последних.
Эволюция любого биологического процесса сопровождается сменой каких-либо его проявлений. Каждое проявление возникает на определенной ступени развития процесса, а затем исчезает через различные периоды времени или персистирует до окончания жизненного цикла индивида. В зависимости от обязательности, сроков и длительности своего существования все возможные проявления любого биологического процесса целесообразно представить в виде следующей классификационной схемы.
Классификация проявлений биологических процессов:
- По обязательности своего развития.
1.1. Облигатные.
1.2. Факультативные. - По времени своего развития.
2.1. Стартовые.
2.2. Промежуточные.
2.3. Финальные. - По длительности своего существования.
3.1. Временные (неперсистирующие).
3.2. Персистирующие.
Облигатными являются физиологические, патоморфологические или постмортальные проявления, обязательно развивающиеся в данном органе или ткани на той или иной стадии эволюции биологического процесса при условии его полного завершения. Примером облигатных проявлений эволюции церебральных повреждений служат макрофагальная реакция и астроцитарный глиоз. В отличие от них факультативные проявления не являются обязательными, то есть, под влиянием случайных обстоятельств возникают только в части случаев реализации данного биологического процесса, в том числе и у одного и того же индивида. К факультативным проявлениям динамики заживления ОПГМ, например, относится гемосидероз.
Стартовые признаки являются первыми (начальными) проявлениями биологического процесса. Примером стартовых проявлений воспалительно-репаративного процесса служит сосудистая реакция. Промежуточные проявления возникают после стартовых, существуют некоторое время, а затем исчезают. В качестве примеров промежуточных проявлений воспалительно-репаративного процесса можно назвать нейтрофильную и макрофагальную реакции. К финальным относятся проявления, завершающие динамику биологического процесса. Финальными проявлениями упомянутого выше воспалительно-репаративного процесса, в частности, являются различные тканевые разновидности рубцевания (фиброз, гиалиноз, петрификация, глиоз).
Временными называются проявления, возникающие на любом этапе течения биологического процесса, но исчезающие впоследствии. Временными всегда являются промежуточные проявления, но временными также могут быть и стартовые, и финальные проявления биологического процесса. К персистирующим относятся проявления, которые, однажды возникнув, затем сохраняются неограниченно долго. Персистирующими могут быть только финальные проявления биологического процесса.
Несмотря на стереотипность каждого биологического процесса кинетике любого из них в отдельно взятых наблюдениях присущи индивидуальные особенности. Это объясняется тем, что каждый раз один и тот же биологический процесс протекает под влиянием большого количества случайных факторов. Поэтому заранее предсказать время возникновения (исчезновения) того или иного качественного проявления (а для факультативных признаков – и сам факт их развития) данного биологического процесса нельзя, так как оно меняется случайным образом от наблюдения к наблюдению. При этом время возникновения (исчезновения) конкретного качественного проявления может принимать любые значения из определенного хронологического интервала на множестве неотрицательных действительных чисел.
Таким образом, с точки зрения математики время возникновения или исчезновения качественных проявлений любых биологических процессов (иными словами, давность последних) представляет собой непрерывную случайную величину.
Основным способом описания случайной величины является задание функции распределения ее вероятностей
\[F(x) = P(\xi < x)\]
где ξ – случайная величина, а x – произвольное действительное число [43,46,50].
Функция распределения непрерывной случайной величины непрерывна и дифференцируема во всех точках, и является первообразной для функции
\[f(x) = F'(x) ,\]
которая называется плотностью распределения вероятностей случайной величины ξ.
На основе дифференциального закона распределения f(x) можно определить вероятность соответствия идентифицируемой давности ξ биологического процесса любому значению на временном промежутке от х1 до х2, вероятность того, что ξ примет значение, не меньше или меньше определенного значения х, а также установить математическое ожидание величины ξ:
\[P({x_1} \le \xi < {x_2}) = \int\limits_{{x_1}}^{{x_2}} {f(x)dx} = F({x_2}) - F({x_1});\]
\[P(\xi \ge x) = \int\limits_{{x}}^{ + \infty } {f(x)dx} ;\]
\[P(\xi < x) = \int\limits_{ - \infty }^{x} {f(x)dx} ;\]
\[M\xi = \int\limits_{ - \infty }^{ + \infty } {xf(x)dx} .\]
Кроме того, возможно решение обратной задачи – определение точных верхних и нижних граней давности ξ для любой требуемой степени вероятности.
Динамика любого биологического процесса включает возникновение и смену не одного, а нескольких явлений, каждое из которых является непрерывной случайной величиной и может быть использовано в качестве экспертного критерия давности. При одновременном применении группы различных экспертных критериев, можно с большой надежностью идентифицировать давность биологического процесса путем сужения ее доверительного временного промежутка. Кроме того, для определения давности биологических процессов можно использовать не только критерии наличия, но и отсутствия определенных качественных проявлений.
Математическое описание качественной кинетики биологических процессов позволяет также объективно оценивать вероятности конкретных версий о соответствии давности актуального процесса с наличием какого-либо его определенного проявления одному из конечного множества заданных значений
\[\{ {x_1},{x_2}, \ldots {x_n}\} :\]
\[P(\xi = {x_i}) = \frac{{f({x_i})}}{{\sum\limits_{i = 1}^{i = n} {f({x_i})} }}.\]
Такой подход актуален для судебных экспертиз, поводом для назначения которых является необходимость определения вероятностей существующих версий о давности юридически значимых событий.
Практическая реализация изложенных принципов математического описания качественной кинетики биологических процессов характеризуется одним существенным затруднением. А именно, на практике качественная оценка кинетики подразумевает отнесение изучаемого процесса в данный конкретный момент времени к одной из двух взаимоисключающих категорий: с наличием или отсутствием какого-либо определенного, доступного регистрации явления. При обнаружении этого явления невозможно судить о предшествующей длительности его существования. В этом случае для построения качественной хронологической модели необходимо исследовать наличие или отсутствие данного проявления в различные сроки биологического процесса, равномерно распределенные на всем промежутке существования последнего. Однако указанный метод позволит получить аппроксимацию плотности распределения вероятностей не возникновения (исчезновения), а обнаружения (отсутствия) конкретных проявлений биологического процесса.
Поскольку построение моделей качественной кинетики производится на основе изучения эмпирических данных, то точность определения давности биологических процессов зависит от степени соответствия типов и параметров моделей распределения их реальным прототипам. Поэтому при моделировании качественной кинетики процессов по аналогии с прогнозными оценками регрессионных моделей следует выделять такие понятия оценок давности, как истинные, модельные и выборочные [49].
В качестве истинных необходимо рассматривать оценки давности процесса, основанные на точном знании дифференциального закона распределения
\[f(x) .\]
Модельными являются оценки давности, полученные с помощью модели распределения
\[\tilde f(x) ,\]
тип которой выбран исследователем в качестве аппроксимации неизвестной истинной функции
\[f(x) .\]
Выборочными являются оценки, полученные с помощью модели распределения
\[\tilde f(x) ,\]
созданной на основе изучения выборочной совокупности данных.
Выборочные оценки давности процесса всегда сходятся по вероятности к их модельным оценкам при неограниченном увеличении объема выборки (n→∞). В отличие от них, модельные оценки сходятся к истинным оценкам только при условии, что модель плотности распределения
\[\tilde f(x) \]
выбрана правильно. В этом случае неточность определения давности объяснялась бы только ограниченностью исследованной выборки и могла бы быть сделана сколько угодно малой при (n→∞). При неправильном выборе типа аппроксимирующей функции
\[\tilde f(x)\]
выборочные оценки давности не будут обладать свойством состоятельности, т.е. при увеличении объема наблюдений выборочные оценки давности не будут сходиться к ее истинным значениям. Однако при моделировании качественной кинетики во многих случаях модельную функцию
\[\tilde f(x)\]
достаточно верно можно определить теоретически, исходя из биологического смысла изучаемого процесса. Статистический же анализ эмпирических данных в этих случаях необходим лишь для определения точечных оценок параметров модельного распределения
\[\tilde f(x)\]
случайной величины ξ, которые будут сходиться к их истинным оценкам при неограниченном увеличении выборки n.
Наиболее актуальными моделями истинных функций f(x) являются следующие типы теоретических распределений, обладающих хорошо изученными математико-статистическими свойствами: нормальное, логнормальное, экспоненциальное и равномерное [46,50,51].
Нормальное распределение характеризуется плотностью
\[f(x) = \frac{1}{{\sigma \sqrt {2\pi } }}\exp \left\{ {\left. { - \frac{{{{(x - \mu )}^2}}}{{2{\sigma ^2}}}} \right\}} \right. ,\]
\[ - \infty < x < + \infty .\]
Параметры μ и σ нормально распределенной случайной величины ξ совпадают с ее математическим ожиданием и стандартным отклонением. Медиана и мода равны математическому ожиданию:
\[M\xi = {\rm{Me}} = {\rm{Mo}} = \mu .\]
Нормальное распределение наилучшим образом подходит для описания унимодальных симметричных распределений. Аппроксимация распределений с положительной асимметрией достигается с помощью логнормального распределения с функцией плотности
\[f(x) = \frac{1}{{x\sigma \sqrt {2\pi } }}\exp \left\{ {\left. { - \frac{{{{(\ln x - \mu )}^2}}}{{2{\sigma ^2}}}} \right\}} \right. ,\]
\[x,\sigma > 0 и \mu \ge 0\]
для которого
\[M\xi = \exp \left\{ {\mu + \frac{1}{2}{\sigma ^2}} \right\},\]
\[{\rm{Me}} = {e^\mu },\]
\[{\rm{Mo}} = \exp \{ \mu - {\sigma ^2}\} .\]
Нормальное и логнормальное (и вообще все «двуххвостовые») распределения пригодны для описания сроков обнаружения промежуточных проявлений биологических процессов.
Наиболее адекватной аппроксимацией кинетики стартовых проявлений является экспоненциальное распределение с плотностью
\[f(x) = \lambda {e^{ - \lambda x}},\] \[x \ge 0\] и \[\lambda > 0\]
для которого
\[M\xi = \frac{1}{\lambda },\]
\[{\rm{Me}} = \frac{1}{\lambda }\ln 2 = \frac{{0,6931}}{\lambda },\]
Mo=0.
Учитывая, что плотность экспоненциального распределения имеет моду в точке 0, то для оценки давности биологического процесса с наличием стартового проявления значение имеет лишь вопрос о вероятности превышения неизвестной давности определенного значения х:
\[P(\xi \ge x) = \lambda \int\limits_x^{ + \infty } {{e^{ - \lambda x}}} dx = {e^{ - \lambda x}}.\]
Отсюда
\[P(\xi < x) = 1 - P(\xi \ge x) = 1 - {e^{ - \lambda x}} \]
и
\[x = \frac{{\ln P(\xi \ge x)}}{{ - \lambda }} .\]
Последнее выражение представляет собой формулу вычисления максимальной давности биологического процесса с наличием определенного стартового проявления для заданной величины статистической ошибки
\[\alpha = P(\xi \ge x) .\]
Последним типом модельного распределения, которое можно достоверно определить исходя из биологической сущности изучаемого проявления, является равномерное распределение. Данный тип включает семейство распределений таких случайных величин, значения которых внутри определенных границ равновероятны. Поэтому свойствами равномерного обладает распределение сроков обнаружения любого персистирующего проявления. Например, в нервной ткани персистирующими являются такие пролиферативные и дистрофические изменения, как гемосидероз, астроцитарный глиоз и наличие амилоидных телец.
Функция плотности распределения вероятностей равномерного распределения имеет вид
\[f(x) = \left\{ \begin{array}{l}{(b - a)^{ - 1}}{\rm{, }}a < x < b\\{\rm{ }}0,{\rm{ }}x < a;{\rm{ }}x > b\end{array} \right. .\]
Математическое ожидание равномерного распределения равно медиане
\[M\xi = {\rm{Me}} = \frac{{b + a}}{2},\]
а мода не определена.
Для персистирующих проявлений биологических процессов параметр b обычно известен и равен времени регистрации данного проявления (для постмортальных явлений или физиологических явлений у живых субъектов) или завершения процесса. Поэтому при установлении давности процессов с наличием персистирующих проявлений, характеризующихся равномерной плотностью распределения, практическое значение имеет лишь определение параметра а. Осуществить статистическое оценивание параметра а равномерного распределения можно следующим образом.
Пусть по результатам исследования получена выборка из n значений давности моделируемого биологического процесса с наличием определенного персистирующего проявления. Осуществим упорядочивание выборки по возрастанию с формированием ряда
\[{x_1} < {x_2} < \ldots < {x_n}.\]
В первом приближении в качестве параметра а можно принять нижний экстремум x1 исследованной выборки. Однако при таком подходе существует риск значительного смещения выборочной оценки x1 распределения
\[\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over f} (x)\]
вправо от параметра а распределения
\[f(x) .\]
Риск и величина указанного смещения будут тем меньше, чем больше объем исследованной выборки. Для оценки данного риска целесообразно использование следующего метода.
Предположим, что анализируемая выборка наблюдений с наличием определенного персистирующего проявления была получена в результате проведения серии из n испытаний, каждое из которых имело лишь два исхода. Один исход регистрировался при
\[x < {x_1},\] второй – при \[x \ge {x_1}.\]
Учитывая, что число испытаний равно n, и исход x \[{P_{1 - \alpha }}(a < {x_1}) \equiv 1 - \sqrt[n]{\alpha }.\] Единственным способом уменьшения величины \[P(a < {x_1})\] является увеличение объема исследованной выборки (рис. 3). Рис. 3. Номограмма определения \[{P_{1 - \alpha }}(a < {x_1}) = 1 - \sqrt[n]{\alpha }\] в зависимости от объема выборки n и величины α. По оси абсцисс – объем выборки, по оси ординат – Сплошной линией показана номограмма для уровня α = 0,05, коротким пунктиром – для α = 0,025, точками – для α = 0,01, длинным пунктиром – для α = 0,001. В отличие от экспоненциального и равномерного распределений при идентификации давности биологических процессов, качественная кинетика которых моделируется симметричными или асимметричными унимодальными «двуххвостовыми» распределениями, практическое значение имеет определение полного спектра оценок давности: математического ожидания, медианы, моды, верхнего и нижнего экстремумов. Следует помнить, что выборочные оценки параметров хронологических распределений, хотя и сходятся к их модельным оценкам при неограниченном увеличении объема выборки, но не совпадают с ними, а также с неизвестными истинными значениями давности. Определение величины возможных смещений может быть достигнуто путем определения соответствующих интервальных оценок любыми известными методами математической статистики [46,51]. Наиболее сложным является определение давности биологических процессов при невозможности теоретического выбора хронологических распределений, исходя из биологической сущности изучаемых проявлений, или невозможности замены неизвестных реальных распределений их эмпирическими аппроксимациями. Доверительные интервалы для значений случайной величины, характеризующейся каким-либо неизвестным или не подчиняющимся нормальному закону распределением, можно определить на основе использования неравенства Чебышева, доказанного в теории вероятностей [46,50]. В терминах статистической совокупности оно имеет следующую трактовку: для любой выборочной совокупности доля значений, попадающих в интервал \[\bar \pm ks\] будет равна, по крайней мере, \[1 - 1/{k^2},\] где k – любое число, большее 1 [50]. Ценность неравенства Чебышева заключается в том, что оно будет верно для любого частотного распределения данных. Однако ценой универсальности данного метода будет довольно значительное снижение точности определения любого биометрического показателя, в том числе и давности моделируемого процесса [48,59]. При невозможности применения неравенства Чебышева точные верхние и нижние грани неизвестных хронологических распределений можно определить аналогично приведенному выше методу оценивания параметра а равномерного распределения. Изложенные принципы математического описания качественной кинетики биологических процессов были многократно использованы автором при моделировании хронологии развития нетравматических внутрижелудочковых кровоизлияний у недоношенных новорожденных [63], воспалительно-репаративной реакции при НЧМТ [64], инфарктов мозга и вторичных внутристволовых кровоизлияний при травматической церебральной компрессии [65,66]. Результатом явилось создание и внедрение в судебно-медицинскую экспертную практику способов определения продолжительности внеутробной жизни недоношенных новорожденных, давности ЧМТ и длительности травматического сдавления и дислокации ГМ. Таким образом, моделирование распределений давности изучаемого процесса с наличием одного или группы различных его проявлений на основе использования эмпирических статистических данных является апробированным методом математического описания качественной кинетики физиологических, патоморфологических и постмортальных процессов при реконструкции их давности. Указанный подход позволяет в количественной вероятностной форме устанавливать давность и продолжительность событий, вследствие чего должен являться обязательным компонентом любых исследований, посвященных созданию способов судебно-медицинского установления давности физиологических, патоморфологических и постмортальных процессов. Изложенный метод целесообразно также использовать для определения на основе использования байесовского подхода вероятностей давности юридически значимых событий в условиях наличия дополнительной следственной информации о предполагаемых сроках их наступления. Приведенные принципы математического описания не исключают возможности разработки альтернативных методов аналитического отражения качественной кинетики биологических процессов в целях последующей реконструкции их давности.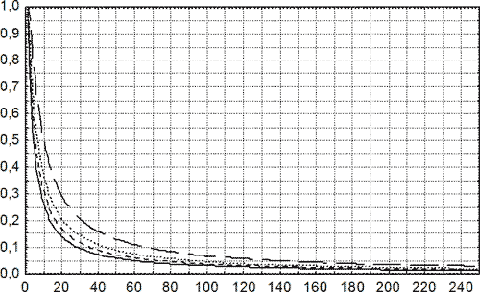
\[{P_{1 - \alpha }}(a < {x_1}).\]

