Вы здесь
1.3. Критерии достоверности диагностических и скрининговых тестов в биомедицине
Понятие достоверности в биомедицине является многозначным и включает в себя комплекс критериев оценки результатов диагностических и скрининговых тестов [9,14,15,54]. К числу основных компонентов данного комплекса относятся следующие характеристики: чувствительность (sensitivity), специфичность (specificity), прогностическая ценность положительного (positive predictive value) и отрицательного (negative predictive value) результатов. Менее актуальны индекс точности (accuracy) и отношение правдоподобия положительного результата (likelihood ratio of a positive test). Каждый критерий представляет собой определенный статистический показатель.
Основная идея статистического оценивания достоверности диагностических и скрининговых тестов заключается в том, что при идентификации актуального патологического или физиологического состояния возможны 4 типа результатов: истинно положительные, ложноположительные, ложноотрицательные и истинно отрицательные. С учетом этого ключевые показатели достоверности диагностических и скрининговых тестов можно охарактеризовать следующим образом.
Обозначим наличие идентифицируемого состояния знаком C, а его отсутствие – знаком противоположного состояния \[\bar C.\] Тогда для оценки достоверности диагностических и скрининговых тестов необходимо исследовать результаты идентификации с помощью оцениваемой медицинской технологии в совокупности объектов объемом n с заведомо известным наличием или отсутствием состояния C.
Пусть a, b, c, d - число зарегистрированных истинно положительных, ложноположительных, ложноотрицательных и истинно отрицательных результатов идентификации состояния С соответственно:
\[n = a + b + c + d.\]
Отсюда общее количество положительных результатов идентификации равно a + b, а отрицательных – c + d. Количество объектов с состоянием С равно a + c, а с альтернативным состоянием \[\bar C – b + d (табл. 1).\]
Таблица 1 Возможные результаты диагностических и скрининговых тестов
| Результат теста | Наличие состояния С | |
| C: a + c | \[\bar C : b + d\] | |
| Положительный a+ b a + 1 - β |
Истинно положительный a 1 - β |
Ложноположительный b α |
| Отрицательный c + d β + 1 - α |
Ложноотрицательный c β |
Истинно отрицательный d 1 - α |
В этом случае критерии достоверности диагностических и скрининговых тестов определяются по формулам:
\[чувствительность - \frac{a}{{a + c}};\]
\[специфичность - \frac{d}{{b + d}};\]
\[ПЦПР - \frac{a}{{a + b}};\]
\[ПЦОР - \frac{d}{{c + d}};\]
\[индекс точности - \frac{{a + d}}{{a + b + c + d}}.\]
Диагностический метод, используемый в качестве эталона определения состояния С и являющийся прототипом для сравниваемой с ним диагностической или скрининговой технологии, называется «золотым стандартом» [9,14,15,54]. В судебной медицине основным «золотым стандартом» являются следственные данные [55].
Рассмотрим изложенные принципы оценивания достоверности диагностических и скрининговых тестов на следующем примере.
Одной из актуальных судебно-медицинских задач является установление генеза (травматический или нетравматический) хронических СГ. Ряд отечественных судебных медиков на основании гистологического исследования капсул 29 хронических СГ известного генеза, полученных в ходе нейрохирургических вмешательств, в качестве способа идентификации травматического генеза хронических СГ предложили критерий наличия комплексов арахноидэндотелия в составе капсулы гематомы [56]. Указанные авторы обнаружили данный признак у 3 из 12 пациентов с нетравматическими и у 4 из 17 потерпевших с травматическими СГ (табл. 2). В качестве «золотого стандарта» определения генеза хронических СГ в указанном исследовании использовались анамнестические данные, изложенные в медицинской документации.
Отсюда чувствительность идентификации травматического генеза хронических СГ по наличию интракапсулярных включений комплексов арахноидэндотелия равна 23,5%, специфичность – 75,0%, ПЦПР – 57,1%, ПЦОР – 40,9%, индекс точности – 44,8%, отношение правдоподобия положительного результата – 0,94.
Таблица 2 Результаты идентификации травматического генеза хронических СГ
| Включения арахноидэндотелия | Генез хронических СГ | Всего | |
| Травматический | Самопроизвольный | ||
| Обнаружены | 4 | 3 | 7 |
| Не обнаружены | 13 | 9 | 22 |
| Итого | 17 | 12 | 29 |
Приведенный показатель чувствительности свидетельствует, что признак наличия интракапсулярных включений арахноидэндотелия не выявляет 76,5% истинных травматических СГ. При этом данный тест правильно идентифицирует 3 из 4 хронических СГ самопроизвольного генеза. ПЦПР означает, что при наличии интракапсулярных включений арахноидэндотелия хроническая СГ в 57% случаев имеет травматический, а в 43% случаев - нетравматический генез. ПЦОР показывает, что при отсутствии интракапсулярных включений арахноидэндотелия хроническая СГ в 41% наблюдений имеет самопроизвольный, а в 59% наблюдений – травматический генез. Индекс точности означает, что правильная диагностика генеза хронических СГ по наличию интракапсулярных включений арахноидэндотелия имеет место лишь в 45% случаев применения данного метода.
Изложенные оценки достоверности показывают, что признак наличия интракапсулярных включений не может использоваться для идентификации генеза хронических СГ, поскольку в 55% приведет к неправильной оценке генеза указанных кровоизлияний.
Важно, что чувствительность и специфичность отражают лишь достоверность идентификации в целом, ничего не говоря об интерпретации результатов идентификации состояний С или \[\bar C\] у конкретного объекта. Поэтому для практики более значимыми являются показатели ПЦПР и ПЦОР, а также индекс точности. ПЦПР и ПЦОР называются также посттестовой вероятностью положительного и отрицательного результатов идентификации соответственно и характеризуют вероятность наличия состояния С у объекта, при исследовании которого зарегистрирован определенный диагностический признак и вероятность отсутствия С (т.е. наличия \[\bar C\]) у объекта, при исследовании которого данный диагностический признак не зарегистрирован.
Существенным недостатком показателей прогностической ценности результатов идентификации и индекса точности является их зависимость от распространенности идентифицируемого состояния С в популяции. Наличие данной зависимости объясняется тем, что в определяющие тождества указанных критериев достоверности входят некоторые частотные показатели обоих идентифицируемых состояний \[С и \bar C\] одновременно. В отличие от данных критериев, подобное вхождение не имеет места в тождествах, определяющих чувствительность и специфичность, вследствие чего последние не зависят от распространенности состояния С.
Так, в приведенном примере доли хронических СГ травматического и самопроизвольного генеза были почти равны (58,6% и 41,4% соответственно). Однако при других соотношениях объектов с наличием или отсутствием идентифицируемого состояния значения показателей прогностической ценности и индекса точности при тех же значениях чувствительности и специфичности идентификации были бы другими (рис. 1).
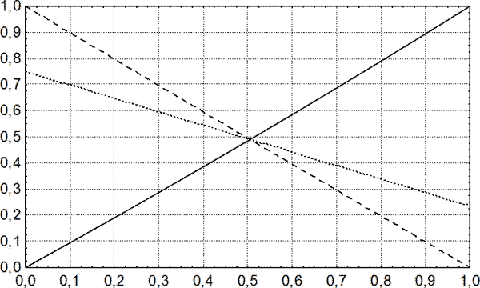
Рис. 1. Зависимость показателей достоверности идентификации травматического генеза хронических СГ от их распространенности. По оси абсцисс – относительная частота травматических хронических СГ; по оси ординат – достоверность идентификации травматического генеза хронических СГ. Сплошной линией показана ПЦПР, пунктирной – ПЦОР, точечной – индекс точности. Чувствительность и специфичность теста фиксированы и равны 0,235 и 0,750 соответственно.
Вследствие указанной зависимости в общем случае любое смещение соотношения априорных частот состояний С и \[\bar C\] в совокупности идентифицируемых объектов от величины, использованной разработчиками диагностического теста при оценивании его достоверности, всегда сопровождается отклонением показателей прогностической ценности и индекса точности от их расчетных значений.
Проблема несоответствия ожидаемых и реальных оценок прогностической ценности имеет место и в клинической медицине, вследствие чего практические врачи совершенно правильно с недоверием относятся к характеристикам прогностической ценности диагностических и скрининговых тестов, заявленным их разработчиками [9].
Изложенное позволило автору предложить альтернативные критерии прогностической ценности, учитывающие распространенность идентифицируемого состояния.
Перед рассмотрением указанных критериев введем понятия априорных вероятностей ложноположительной и ложноотрицательной идентификации состояния С. По сложившейся в математической статистике традиции обозначим указанные вероятности буквами α и β:
\[\alpha = \frac{b}{{b + d}},\]
\[\beta = \frac{c}{{a + c}}.\]
Обозначим также буквами Γ и Δ общепринятые в биомедицине прогностические вероятности ложноположительной и ложноотрицательной идентификации С:
\[\Gamma = 1 - \frac{a}{{a + b}} = \frac{b}{{a + b}},\]
\[\Delta = 1 - \frac{d}{{c + d}} = \frac{c}{{c + d}}. (1)\]
Благодаря указанным понятиям и обозначениям можно формализовать названия ключевых критериев достоверности идентификации: чувствительность - 1 - β, специфичность - 1 - α, ПЦПР - 1 - Г , ПЦОР - 1 - Δ.
Альтернативные критерии достоверности представляют собой апостериорные вероятности ложноположительной и ложноотрицательной идентификации, обозначенные автором буквами γ и δ:
\[\gamma = \frac{\alpha }{{\alpha + 1 - \beta }},\]
\[\delta = \frac{\beta }{{\beta + 1 - \alpha }}.\]
При оценивании достоверности любых диагностических и скрининговых технологий апостериорные вероятности ложноположительной и ложноотрицательной идентификации состояния С эквивалентны прогностическим вероятностям указанных ошибок тогда и только тогда, когда количество объектов с наличием состояния С в тестовой выборке равно количеству объектов с отсутствием данного состояния:
\[\left\{ {a + c = b + d} \right\} \to \left\{ {[\gamma = \Gamma ] \wedge [\delta = \Delta ]} \right\}.\]
Доказательство данного утверждения приведено в работе [48].
С помощью предложенных понятий показатели прогностической ценности положительного и отрицательного результатов формульно характеризуются как 1 - γ и 1 - δ. Указанные характеристики постоянны и не зависят от распространенности состояния С в совокупности идентифицируемых объектов. Тем не менее, для определения показателей прогностической ценности на практике необходимы иные критерии, учитывающие априорную распространенность С.
Пусть P(C) - априорная вероятность (распространенность) состояния С, а \[P(\bar C)\] - аналогичная вероятность противоположного состояния \[\bar C.\] В этом случае полная группа возможных результатов идентификации С формализуется записью
\[P(\bar C) \cdot \alpha + P(\bar C) \cdot (1 - \alpha ) + P(C) \cdot \beta + P(C) \cdot (1 - \beta ) = 1.\]
Тогда апостериорные вероятности ложноположительной (ε) и ложноотрицательной (ζ) идентификации, учитывающие распространенность С в совокупности идентифицируемых объектов, определяются по формулам:
\[\varepsilon = \frac{{P(\bar C) \cdot \alpha }}{{P(\bar C) \cdot \alpha + P(C) \cdot (1 - \beta )}},\]
\[\zeta = \frac{{P(C) \cdot \beta }}{{P(C) \cdot \beta + P(\bar C) \cdot (1 - \alpha )}}.\]
В свою очередь, модификации показателей ПЦПР и ПЦОР, учитывающие распространенность С в совокупности идентифицируемых объектов, следует вычислять как 1 - ε и 1 - 1 - ζ. Множества значений и 1 - ζ на отрезке [0,1] возможных значений P(C) при фиксированных показателях чувствительности и специфичности будут иметь вид номограмм, подобных приведенным на рисунке 1.
Легко доказать [48], что при равенстве априорных вероятностей идентифицируемого состояния С и противоположного ему состояния апостериорные вероятности ложноположительной и ложноотрицательной идентификации γ и δ эквивалентны ошибкам ε и ζ:
\[\left\{ {P(C) = P(\bar C)} \right\} \to \left\{ {[\gamma = \varepsilon ] \wedge [\delta = \zeta ]} \right\}.\]
Изложенное имеет важное научное и прикладное значение. В рамках первого компонента приведенные данные прямо определяют следующий методологический дизайн тестирования достоверности диагностических и скрининговых тестов:
- количество объектов с наличием идентифицируемого состояния С должно равняться количеству объектов с его отсутствием;
- ошибки идентификации состояния С должны быть представлены оценками α, β, γ и δ, а критерии достоверности диагностических тестов – оценками 1- α, 1 - β, 1 - γ и 1 - δ;
- после вычисления оценок γ и δ должны быть разработаны номограммы определения ошибок ε и ζ и соответствующих значений прогностической ценности результатов положительной и отрицательной идентификации 1 - ε и 1 - ζ для континуума значений P(C) на отрезке [0;1] при фиксированных значениях 1 - α и 1 - β.
Для практической судебно-медицинской деятельности приведенные утверждения означают, что формулирование выводов относительно степени достоверности идентификации должно осуществляться с учетом априорной вероятности идентифицируемого состояния P(C) по соответствующим номограммам, подобным приведенной на рисунке 1. В случае отсутствия указанных номограмм в пакете услуг, предоставляемых разработчиком диагностической технологии, первые могут быть созданы самим экспертом, исходя из данных о чувствительности, специфичности и апостериорных ошибках идентификации. Отсутствие информации об указанных оценках, равно как и незнание или недостаточность теоретических предположений относительно распространенности идентифицируемого состояния в совокупности исследуемых объектов является противопоказанием к практическому использованию данной технологии идентификации. Важно подчеркнуть, что большинство судебно-медицинских диагностических технологий предполагают одинаковые априорные вероятности наличия и отсутствия состояния С, в то время как это условие далеко не всегда выполняется на практике.
Необходимо также обратить внимание, что при большой распространенности идентифицируемого состояния ПЦПР любого диагностического теста увеличивается. В предельном случае
\[\left\{ {P(C) = 1} \right\} \to \left\{ {\Gamma = 0} \right\}.\]
Последнее выражение характеризует парадоксальную ситуацию, когда при отсутствии объектов с альтернативным состоянием ПЦПР любого, даже недостоверного теста, равна 1 (см. рис. 1). Данное положение аналогично ситуации, в которой сломанные часы два раза в сутки все же показывают правильное время.
По своей сути ключевые критерии достоверности диагностических и скрининговых тестов представляют собой относительные частотные показатели. Так, чувствительность представляет собой долю истинно положительных результатов идентификации в совокупности объектов с наличием идентифицируемого состояния, специфичность – долю истинно отрицательных результатов в совокупности объектов с отсутствием идентифицируемого состояния. ПЦПР представляет собой долю истинно положительных результатов в совокупности всех положительных результатов идентификации, ПЦОР – долю истинно отрицательных результатов в совокупности всех отрицательных результатов идентификации.
Ввиду невозможности исследования разработчиками диагностических технологий генеральных совокупностей объектов все перечисленные критерии достоверности определяются с использованием тестовых выборок ограниченного объема. В этой связи для исчерпывающего суждения о достоверности диагностического теста необходимо вычисление интервальных оценок каждого критерия последней. Данная рекомендация соответствует общей тенденции к расширению показаний к применению ДИ в биомедицинских исследованиях вплоть до замены ими обычных статистических критериев [9,28,58].
Таким образом, определение интервальных оценок чувствительности и специфичности должно стать обязательным компонентом любой программы тестирования достоверности диагностических и скрининговых технологий. К сожалению, определение интервальных оценок для наиболее значимых критериев достоверности – ПЦПР и ПЦОР является затруднительным. Это объясняется тем, что простое вычисление доверительных границ для указанных критериев не имеет смысла, поскольку как уже было показано, их точечные оценки сильно зависят от распространенности идентифицируемого состояния С.
В этой связи весьма актуальной является проблема определения доверительных границ для критериев достоверности γ, δ, ε и ζ. Трудность поставленной задачи определяется тем, что в определяющие тождества данных критериев входят точечные оценки сразу двух параметров одновременно: α и β. Вследствие этого в литературе даже высказывалось мнение о невозможности общего решения подобных проблем и предлагались отдельные решения ее частных случаев [59].
Изложенное позволило предложить метод определения доверительных границ для каждого из указанных критериев достоверности [48], суть которого сводится к следующему.
Сначала при выбранном уровне значимости вычисляют интервальные оценки показателей α и β:
\[\alpha \in \left[ {{\alpha _{\min }};{\alpha _{\max }}} \right]и\]
\[\beta \in \left[ {{\beta _{\min }};{\beta _{\max }}} \right].\]
Интервальные оценки для γ с надежностью не менее 1 - 2α определяются как
\[\gamma \in \left[ {{\gamma _{\min }};{\gamma _{\max }}} \right], где\]
\[{\gamma _{\min }} = \frac{{{\alpha _{\min }}}}{{{\alpha _{\min }} + 1 - {\beta _{\min }}}},\]
\[{\gamma _{\max }} = \frac{{{\alpha _{\max }}}}{{{\alpha _{\max }} + 1 - {\beta _{\max }}}}.\]
Интервальные оценки ε при уровне надежности не менее 1 – 2α определяются по формуле:
\[\varepsilon \in \left[ {{\varepsilon _{\min }};{\varepsilon _{\max }}} \right],\]
где
\[{\varepsilon_{\min }} = \frac{{P(\bar C){\alpha _{\min }}}}{{P(\bar C){\alpha _{\min }} + P(C)(1 - {\beta _{\min }})}},\]
\[{\varepsilon _{\max }} = \frac{{P(\bar C){\alpha _{\max }}}}{{P(\bar C){\alpha _{\max }} + P(C)(1 - {\beta _{\max }})}}.\]
Интервальные оценки для δ с надежностью не менее 1 - 2 α определяются как
\[\delta \in \left[ {{\delta _{\min }};{\delta _{\max }}} \right], где\]
\[{\delta _{\min }} = \frac{{{\beta _{\min }}}}{{{\beta _{\min }} + 1 - {\alpha _{\min }}}},\] \[{\delta _{\max }} = \frac{{{\beta _{\max }}}}{{{\beta _{\max }} + 1 - {\alpha _{\max }}}}.\]
В свою очередь, интервальные оценки ζ с надежностью не менее 1 - 2 α принадлежат промежутку \[\zeta \in \left[ {{\zeta _{\min }};{\zeta _{\max }}} \right], где\]
\[{\zeta _{\min }} = \frac{{P(C){\beta _{\min }}}}{{P(C){\beta _{\min }} + P(\bar C)(1 - {\alpha _{\min }})}},\]
\[{\zeta _{\max }} = \frac{{P(C){\beta _{\max }}}}{{P(C){\beta _{\max }} + P(\bar C)(1 - {\alpha _{\max }})}}.\]
Используя оценки γ, δ, ε и ζ, с надежностью не менее 1 – 2a определяют интервальные оценки критериев достоверности:
\[\{ 1 - \gamma \} \in \left[ {1 - {\gamma _{\max }};1 - {\gamma _{\min }}} \right],\]
\[\{ 1 - \delta \} \in \left[ {1 - {\delta _{\max }};1 - {\delta _{\min }}} \right],\]
\[\{ 1 - \varepsilon \} \in \left[ {1 - {\varepsilon _{\max }};1 - {\varepsilon _{\min }}} \right]\] при \[P(C) \in \left[ {0;1} \right],\]
\[\{ 1 - \zeta \} \in \left[ {1 - {\zeta _{\max }};1 - {\zeta _{\min }}} \right]\] при \[P(C) \in \left[ {0;1} \right].\]
Интервальные оценки основных критериев достоверности идентификации генеза хронических СГ приведены в таблице 3.
Таблица 3 Точечные и 95% двусторонние интервальные оценки критериев достоверности идентификации травматического генеза хронических СГ по наличию интракапсулярных включений арахноидэндотелия
| α | 0,055 | 0,250 | 0,572 |
| β | 0,501 | 0,765 | 0,932 |
| Γ | 0,099 | 0,429 | 0,816 |
| Δ | 0,364 | 0,591 | 0,793 |
| γ | 0,099 | 0,515 | 0,894 |
| δ | 0,346 | 0,505 | 0,685 |
| 1 - β | 0,068 | 0,235 | 0,499 |
| 1 - α | 0,428 | 0,750 | 0,945 |
| 1 - Γ | 0,184 | 0,571 | 0,901 |
| 1 - Δ | 0,207 | 0,409 | 0,636 |
| 1 - γ | 0,106 | 0,485 | 0,901 |
| 1 - δ | 0,315 | 0,495 | 0,654 |
При необходимости интервальные оценки ПЦПР и ПЦОР могут быть вычислены и с учетом распространенности идентифицируемого состояния С в совокупности объектов идентификации. Ввиду непрерывности множества указанных оценок результаты их вычисления целесообразно представлять в форме номограмм [57]. Например, номограмма определения точечных и интервальных оценок прогностической ценности результатов положительной идентификации травматического генеза хронических СГ по наличию интракапсулярных включений арахноидэндотелия в зависимости от распространенности СГ данного генеза приведена на рисунке 2.
Важно подчеркнуть, что анализируемые диагностические и скрининговые биомедицинские тесты предполагают так называемую биномиальную схему идентификации, согласно которой диагностическая технология относит объект идентификации к одному из двух классов: с наличием актуального состояния или с его отсутствием. Помимо биномиальной в судебно-медицинской практике часто имеет место так называемая полиномиальная схема идентификации [48,59]. Процедура последней сводится к отнесению идентифицируемого объекта к одному из нескольких заранее известных классов, количество которых более двух. При этом множество дифференцируемых классов конечно и образует полную группу. Полиномиальная схема идентификации характерна для судебно-антропологических научных и экспертных исследований, посвященных разработке способов установления соматотипа, расы и порядковой локализации однотипных костей [59].
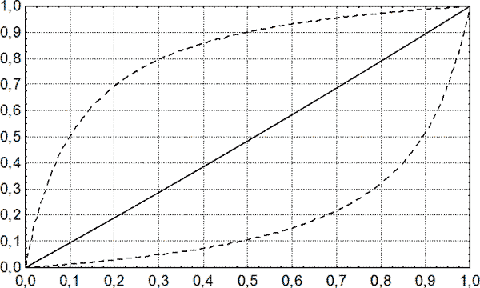
Рис. 2.Номограмма определения точечных и 95% интервальных оценок ПЦПР идентификации травматического генеза хронических СГ при различной их распространенности. По оси абсцисс – относительная частота травматических хронических СГ; по оси ординат – ПЦПР идентификации травматического генеза. Сплошной линией показаны точечные, пунктирными – 95% двусторонние интервальные оценки. Чувствительность и специфичность теста фиксированы и равны 0,235 и 0,750 соответственно.
Аналитическая процедура оценивания достоверности полиномиальной идентификации достаточно полно разработана [48], однако в данном разделе не рассматривается, поскольку пока не имеет приложений в судебно-медицинской нейротравматологии. Алгоритм оценивания достоверности полиномиальной идентификации также может быть обобщен на случай выделения степеней категоричности экспертных суждений [59].
Таким образом, на современном этапе развития судебной медицины и биомедицины в целом разработка любых диагностических или скрининговых технологий должна включать обязательное точечное и интервальное оценивание ключевых критериев достоверности. Наличие подобного тестирования является необходимым условием для внедрения новой диагностической технологии в медицинскую практику. В этой связи в судебной медицине помимо создания новых технологий актуальными также представляются исследования достоверности диагностических методик и признаков, ставших известными до распространения принципов доказательной медицины и уже укоренившихся в практической экспертной деятельности. Изложенные принципы подразумевают внесение соответствующих дополнений в систему подготовки судебно-медицинских экспертов.

