4.2. Математические принципы реконструкции давности событий

Разработка объективных критериев для установления давности и продолжительности событий, проявляющихся различными физиологическими, патоморфологическими или постмортальными изменениями, является одним из приоритетных научных направлений в судебной медицине [81]. На этом, в частности, базируется экспертное определение давности и прижизненности повреждений. В общем виде методология решения указанного вопроса основывается на данных о стадийности изменчивости исследуемого физиологического, патоморфологического или постмортального процесса и сводится к качественному выявлению и количественному оцениванию различных его проявлений [85].

В настоящее время общепризнанным считается, что количественные методы определения давности каких-либо физиологических, патоморфологических или постмортальных процессов потенциально наиболее информативны [7,107]. Стандартным подходом к решению проблемы реконструкции давности событий, сопровождающихся количественно измеряемыми изменениями, является использование методов регрессионного анализа.

Однако до сих пор значительная часть вопросов судебно-медицинского определения давности событий по-прежнему решается только путем качественного оценивания их различных проявлений. При этом полученные данные справедливо расцениваются лишь как приблизительные и имеют небольшое доказательное значение [81,107]. Вместе с тем, не следует забывать, что качественная оценка кинетики любых актуальных процессов по сравнению с количественными методами исследования отличается двумя преимуществами: малой трудоемкостью и хорошей воспроизводимостью. Кроме того, ориентировочный характер результатов качественных исследований во многом объясняется отсутствием теоретического осмысления сущности изучаемых явлений в строгой математической форме. Указанные обстоятельства свидетельствуют о преждевременности принципиального отказа от качественных методов судебно-медицинского определения давности событий, сопровождающихся различными физиологическими, патоморфологическими или постмортальными изменениями.

В этой связи перспективным и необходимым методом изучения качественной кинетики любых процессов, запущенных наступлением события, актуального в плане определения его давности, представляется вероятностное математическое описание (моделирование) качественных особенностей хронологии аналогичных (повторяемых) событий. При этом математическое моделирование качественной кинетики процессов позволит объективно оценивать их давность и использовать полученные оценки для решения соответствующих экспертных задач.

В связи с изложенным приводим теоретическое обоснование основных принципов вероятностной реконструкции давности качественных физиологических, патоморфологических и постмортальных процессов, которые в дальнейшем для краткости условимся именовать термином «моделируемые процессы».

Пусть требуется установить давность t события, наступление которого сопровождается инициализацией гипотетического моделируемого процесса. При отсутствии какой-либо информации о проявлениях данного процесса t может соответствовать любому значению, принадлежащему полуоткрытому промежутку \([0;{t_{\max }})\) при \({t_{\max }} \to + \infty \).

Допустим, что эволюция моделируемого процесса включает определенное явление (экспертный критерий) х. Явление х возникает на определенной ступени развития процесса, а затем исчезает через различные периоды времени или длительно персистирует. Качественная оценка кинетики в этом случае подразумевает отнесение изучаемого процесса к одной из двух взаимоисключающих категорий: с наличием или отсутствием явления х.

Проблемным моментом для моделирования качественной кинетики процессов является тот факт, что при обнаружении х невозможно судить о предшествующей длительности его существования. Данное затруднение может быть преодолено путем объединения теоретических принципов математического моделирования с результатами практических наблюдений (статистическими данными). В этом случае для построения качественной хронологической модели необходимо исследовать наличие х в различные сроки моделируемого процесса, равномерно распределенные на промежутке \([0;{t_{\max }})\).

В итоге этого исследования будет получено распределение сроков патоморфологического процесса с наличием х, которое является непрерывным. Тогда вероятность того, что идентифицируемая давность процесса \({x_t} < x\), зависит от х и является интегральной функцией распределения: \(F(x) = P({x_t} < x)\), обладающей следующими основными свойствами:

1. \(0 \le F(x) \le 1\);
2. если \({x_2} > {x_1}\), то \(F({x_2}) \ge F({x_1})\);
3. \(\mathop {\lim }\limits_{x \to - \infty } F(x) = 0\); \(\mathop {\lim }\limits_{x \to + \infty } F(x) = 1\).

имеет производную в любой точке х и является первообразной для функции \(f(x)\): \(f(x) = F'(x)\).

Функция \(f(x)\) характеризует плотность, с которой распределены значения вероятности случайной величины х в данной точке временного промежутка, и является дифференциальной функцией распределения, обладающей следующими важными свойствами: \(f(x) \ge 0\); \(\int\limits_{ - \infty }^{ + \infty } {f(x)dx = 1} \).

В случае положительной диагностики явления х на основе дифференциального закона распределения \(f(x)\) можно определить вероятность соответствия идентифицируемой давности \({x_t}\) моделируемого процесса любому значению на временном промежутке \(\left[ {{x_1};{x_2}} \right]\), вероятность превышения \({x_t}\) определенного значения \({x_{\max }}\), вероятность того, что \({x_t}\) не превысит определенное значение \({x_{\min }}\), а также установить математическое ожидание величины х:

\[P({x_1} \le {x_t} \le {x_2}) = \int\limits_{{x_1}}^{{x_2}} {f(x)dx} = F({x_2}) - F({x_1});\]

\[P({x_t} \ge {x_{\max }}) = \int\limits_{{x_{\max }}}^{ + \infty } {f(x)dx};\]

\[P({x_t} \le {x_{\min }}) = \int\limits_{ - \infty }^{{x_{\min }}} {f(x)dx};\]

\[\mu = E(x) = \int\limits_{ - \infty }^{ + \infty } {xf(x)dx}.\]

Кроме того, возможно решение обратной задачи – определение концов числового промежутка \(\left[ {{x_1};{x_2}} \right]\), а также значений \({x_{\max }}\) или \({x_{\min }}\) для любой требуемой степени вероятности.

Как правило, динамика моделируемого процесса включает возникновение и смену не одного, а нескольких явлений \({x_i}\), \(i = 1,2, \ldots ,n\), каждое из которых характеризуется функцией плотности распределения \(f({x_i})\). При одновременном использовании функций \(f({x_i})\) группы различных экспертных критериев, можно с большой надежностью идентифицировать давность моделируемого процесса путем определения ее принадлежности узкому временному промежутку \(\left[ {{t_{\min }};{t_{\max }}} \right]\). Кроме того, для определения давности моделируемого процесса можно использовать не только критерии наличия, но и отсутствия явления \({x_i}\).

Поскольку построение моделей качественной кинетики производится на основе изучения эмпирических данных, то точность определения давности моделируемых процессов зависит от степени соответствия типов и параметров моделей распределения \(f({x_i})\) их реальным прототипам. Поэтому при моделировании качественной кинетики процессов по аналогии с прогнозными оценками регрессионных моделей следует выделять такие понятия оценок давности, как истинные, модельные и выборочные [29,60].

В качестве истинных необходимо рассматривать оценки давности процесса, основанные на точном знании дифференциального закона распределения \(f({x_i})\). Модельными являются оценки давности, полученные с помощью модели распределения \(\tilde f({x_i})\), тип которой выбран исследователем в качестве аппроксимации неизвестной истинной функции \(f({x_i})\). Выборочными являются оценки, полученные с помощью модели распределения \(\tilde f({x_i})\), созданной на основе изучения выборочной совокупности данных.

Выборочные оценки давности процесса всегда сходятся по вероятности к их модельным оценкам при неограниченном увеличении объема выборки \((n \to \infty )\). В отличие от них, модельные оценки сходятся к истинным оценкам только при условии, что модель функции плотности распределения \(\tilde f({x_i})\) выбрана правильно. В этом случае неточность определения давности объяснялась бы только ограниченностью исследованной выборки и могла бы быть сделана сколько угодно малой при \((n \to \infty )\). При неправильном выборе типа аппроксимирующей функции \(\tilde f({x_i})\) выборочные оценки давности не будут обладать свойством состоятельности, т.е. при увеличении объема наблюдений выборочные оценки давности не будут сходиться к ее истинным значениям. Однако при моделировании качественной кинетики во многих случаях модельную функцию \(\tilde f({x_i})\) достаточно верно можно определить теоретически, исходя из биологического смысла изучаемого процесса и его проявлений \({x_i}\). Статистический же анализ эмпирических данных в этих случаях необходим лишь для определения точечных оценок параметров модельного распределения \(\tilde f({x_i})\) случайной величины \({x_i}\), которые будут сходиться к их истинным оценкам при неограниченном увеличении выборки n.

Изложенные принципы реконструкции давности событий можно пояснить на примере математического моделирования качественной кинетики воспалительно-репаративной реакции в очагах ушиба головного мозга, проведенного нами в целях определения давности закрытой и открытой непроникающей черепно-мозговой травмы. Методы, объекты и результаты данного исследования подробно охарактеризованы нами ранее [63].

Согласно современным представлениям эволюция ушибов головного мозга слагается из фаз экссудации, пролиферации и репарации, отличаясь от стереотипной воспалительно-репаративной реакции лишь индивидуальностью типов клеточных популяций, последовательно доминирующих в морфогенезе [15,49,52,75,108,109]. Экссудация в очагах ушиба представлена микроциркуляторной, медиаторной и нейтрофильной реакциями. На светооптическом уровне указанные реакции документируются наличием гиперемии, набухания олигодендроглии, эритроцитарной имбибиции периваскулярной нервной ткани в зонах кровоизлияний, экссудативного воспаления различной степени выраженности, кольцевидных кровоизлияний, отека и некрозов. Фаза пролиферации воспалительно-репаративной реакции морфологически проявляется формированием отграничительного вала из зернистых шаров и зоны ангиоматоза. Маркерами фазы рубцевания являются выраженное увеличение количества и резкая гипертрофия астроцитов с образованием волокнообразующих астроцитов в перифокальных к некротизированным и резорбирующимся очагам ушиба отделах головного мозга.

Статистический анализ 37 наблюдений летальной черепно-мозговой травмы показал, что хронология экссудативной фазы воспалительно-репаративной реакции в очагах ушиба мозга при отсутствии зернистых шаров и роста сосудов хорошо аппроксимируется экспоненциальным распределением с функцией плотности
\(f(x) = A{e^{ - Ax}}\), где \(A = 0,01413725\) (рис. 6).

Поскольку экссудация в контузионных очагах головного мозга развивается практически сразу же после их причинения, то полученная на основе анализа статистических данных математическая модель хорошо отражает биологический смысл данной фазы воспалительно-репаративной реакции. Учитывая, что плотность экспоненциального распределения имеет моду в точке 0, то для оценки давности черепно-мозговой травмы с наличием данного морфологического критерия практическое значение имеет лишь вопрос о вероятности превышения \({x_t}\) определенного значения \({x_{\max }}\).

Пусть \({x_{\max }} = {x_0}\), тогда \(P({x_t} \ge {x_0}) = A\int\limits_{{x_0}}^{ + \infty } {{e^{ - Ax}}} dx = {e^{ - A{x_0}}}. (1)\)

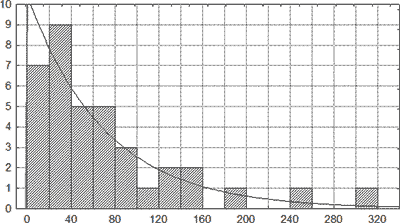
Рис. 6.Распределение сроков изолированной экссудативной фазы воспалительно-репаративного процесса в очагах ушиба головного мозга. По оси абсцисс – давность черепно-мозговой травмы, ч; по оси ординат – количество наблюдений.

Отсюда \(P({x_t} \le {x_0}) = 1 - P({x_t} \ge {x_0}) = 1 - {e^{ - A{x_0}}}\).

Например, вычислим вероятность длительности изолированной экссудативной фазы воспалительно-репаративной реакции в контузионных очагах головного мозга 120 ч или более: \(P({x_t} \ge 120) = {e^{ - 0,01413725 \cdot 120}} = 0,183\), а также вероятность длительности данной фазы воспалительно-репаративной реакции не более 120 ч: \(P({x_t} \le {x_0}) = 1 - 0,183 = 0,817\).

Вычисленные значения Р тождественны значениям доли наблюдений черепно-мозговой травмы, в которых длительность изолированной экссудативной фазы воспалительно-репаративной реакции составляет не менее или не более 120 ч соответственно.

Из выражения (1) легко получить формулу вычисления максимальной давности черепно-мозговой травмы с наличием изолированной экссудативной фазы воспалительно-репаративной реакции для определенной доверительной вероятности \(\alpha = P({x_t} \ge {x_{\max }})\): \({x_{\max }} = \frac{{\ln P({x_t} \ge {x_{\max }})}}{{ - A}}\).

Например, при 95% уровне надежности максимальная давность черепно-мозговой травмы с наличием изолированной экссудативной фазы воспалительно-репаративной реакции составляет

\[{x_{\max }} = \frac{{\ln 0,05}}{{ - 0,01413725}} = 211,9 ч.\]

Другим типом модельного распределения \(\tilde f({x_i})\), которое можно достоверно определить теоретически, исходя из биологической сущности изучаемого проявления \({x_i}\), является равномерное распределение. Данный тип включает семейство распределений таких случайных величин, значения которых внутри определенных границ равновероятны. Например, равномерным является распределение сроков моделируемых процессов с наличием любого явления \({x_i}\), характеризующегося появлением на определенной стадии процесса и последующей длительной персистенцией. В качестве хронически персистирующих в нервной ткани проявлений воспалительно-репаративной реакции можно назвать такие маркеры ее пролиферативной и репаративной фаз, как гемосидероз, астроцитарный глиоз и наличие амилоидных телец [16].

Рассмотрим хронологическую модель репаративной фазы воспалительно-репаративной реакции в контузионных очагах головного мозга с астроцитарным глиозом в качестве критерия х. Учитывая персистенцию глиального рубца на протяжении всего периода жизни индивида, случайная величина х (давность моделируемого процесса с наличием астроцитарного глиоза) равномерно распределена на временном промежутке от \({x_{\min }}\) до \({x_{\max }}\). Тогда плотность распределения х является константой на промежутке \(\left[ {{x_{\min }};{x_{\max }}} \right]\) и равна нулю вне этого промежутка:

\[f(x) = \left\{ \begin{array}{l}c{\kern 2pt}{\rm{ при }}{\kern 2pt}{x_{\min }} \le {x_t} \le {x_{\max }}\\0{\kern 2pt}{\rm{ при }}{\kern 2pt}{x_t} < {x_{\min }}{\kern 2pt}{\rm{ или }}{\kern 2pt}{x_t} > {x_{\max }}\end{array} \right.,(2)\]

где \(c = 1/({x_{\max }} - {x_{\min }})\).

Учитывая, что \({x_{\max }} \to + \infty \), то для равномерной плотности \(f(x)\) можно принять \(x \in [{x_{\min }}; + \infty )\). Тогда формулу (2) можно записать как

\[f(x) = \left\{ \begin{array}{l}c{\kern 2pt}{\rm{ при }}{\kern 2pt}{x_{\min }} \le {x_t}\\0{\kern 2pt}{\rm{ при }}{\kern 2pt}{x_t} < {x_{\min }}\end{array} \right..\]

Ввиду незамкнутости числового промежутка \(x \in [{x_{\min }}; + \infty )\) для установления давности моделируемого процесса с наличием проявления х, характеризующегося равномерной плотностью распределения, практическое значение имеет лишь определение величины \({x_{\min }}\).

Пусть по результатам исследования получена выборка из n значений давности моделируемого процесса с наличием проявления х. Осуществим упорядочивание выборки по возрастанию х с формированием ряда \({x_1} < {x_2} < \ldots < {x_n}\). В первом приближении в качестве \({x_{\min }}\) можно принять нижний экстремум \({x_1}\) исследованной выборки. Однако при таком подходе существует риск значительного смещения выборочной оценки \({x_1}\) распределения \(\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over f} (x)\) вправо от параметра \({x_{\min }}\) распределения \(f(x)\). Риск и величина указанного смещения будут тем меньше, чем больше объем исследованной выборки. Для оценки данного риска целесообразно использование следующего метода.

Предположим, что анализируемая выборка была получена в результате проведения серии из n испытаний, каждое из которых имело лишь два исхода. Один исход регистрировался при \({x_0} < {x_1}\), второй – при \({x_0} \ge {x_1}\). Учитывая, что число испытаний равно n, и исход \({x_0} < {x_1}\) не наблюдался ни разу, то с помощью точных доверительных границ для биномиального распределения можно вычислить требуемую \(1 - \alpha \) надежность оценки параметра \({x_{\min }}\): \(P({x_0} < {x_1}) = 1 - \sqrt[n]{\alpha }\).

Например, по данным проведенного исследования качественной кинетики воспалительно-репаративной реакции в контузионных очагах головного мозга астроцитарный глиоз был обнаружен нами в 9 наблюдениях. При этом минимальное выборочное значение давности воспалительно-репаративной реакции с наличием астроцитарного глиоза равнялось 9 суткам \(({x_1} = 9)\). Отсюда с 95% доверительной надежностью делаем вывод, что вероятность обнаружения астроцитарного глиоза ранее 9 суток достаточно высока и равна

\[P({x_0} < {x_1}) = 1 - \sqrt[9]{{0,05}} = 0,283.\]

При этом единственным способом уменьшения величины \(P({x_0} < {x_1})\) является увеличение объема исследованной выборки (рис. 7).

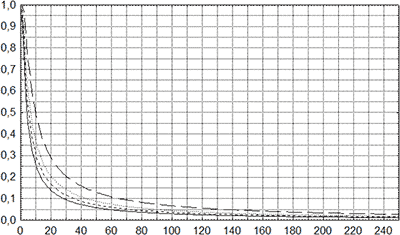
Рис. 7. Номограмма определения \(P({x_0} < {x_1}) = 1 - \sqrt[n]{\alpha }\) в зависимости от объема выборки n и величины α. По оси абсцисс – объем выборки, по оси ординат – вероятность. Сплошной линией показана номограмма для \(\alpha = 0,05\), коротким пунктиром – для \(\alpha = 0,025\), точками – для \(\alpha = 0,01\), длинным пунктиром – для \(\alpha = 0,001\).

Наиболее сложным является моделирование распределений, тип которых не может быть достоверно определен теоретически. В этих случаях необходима аппроксимация статистических данных каким-либо распределением, для которого можно определить функцию плотности. Например, статистический анализ 23 наблюдений летальной черепно-мозговой травмы показал, что распределение сроков наличия зернистых шаров в очагах ушиба головного мозга является унимодальным и характеризуется выраженной положительной асимметрией (рис. 8).

Удобной моделью для подобных типов данных является логнормальное распределение с функцией плотности
\(f(x) = \frac{1}{{\sqrt {2\pi } \cdot \sigma x}}{e^{ - \frac{{{{(\ln x - \mu )}^2}}}{{2{\sigma ^2}}}}}\), где \(\mu = \sum\limits_{i = 1}^N {\ln {x_i}} /N\); \(\sigma = \sqrt {\sum\limits_{i = 1}^N {{{(\ln {x_i} - \mu )}^2}/N} } \), а N – объем выборки [126].

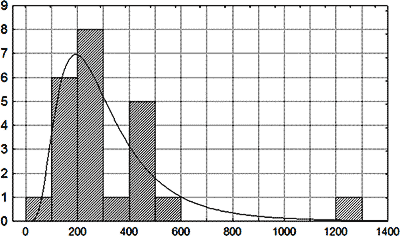
Рис. 8. Распределение сроков наличия зернистых шаров в контузионных очагах головного мозга. По оси абсцисс – давность черепно-мозговой травмы, ч; по шкале ординат – количество наблюдений.
В отличие от экспоненциального и равномерного распределений при идентификации давности процессов, моделируемых симметричными или асимметричными унимодальными «двуххвостовыми» распределениями практическое значение имеет лишь определение типичного значения (медианы) и интервальных оценок величины х.

Для модели логнормального распределения оценка медианы х тождественна значению параметра масштаба μ дифференциального закона распределения \(f(x)\). Доверительные интервалы для значений х можно определить, предварительно вычислив соответствующие интервальные оценки величины \(\ln x\) с последующим их преобразованием с помощью выражения \({e^{\ln x}}\).

В нашем примере точечные оценки параметров масштаба и формы для логнормальной модели распределения сроков давности воспалительно-репаративной реакции в контузионных очагах головного мозга с наличием зернистых шаров составили \(\bar x = 5,598\) и \(s = 0,577\). Отсюда точечная оценка медианы давности ушибов головного мозга с наличием зернистых шаров равна \(\tilde x = {e^{5,598}} = 270\) ч. Доверительный интервал для медианы может быть вычислен непосредственно или опосредованно через преобразования интервальных оценок параметра масштаба, рассчитанных с помощью t-распределения. В последнем случае \((100 - \alpha )\)% доверительный интервал для медианы определяется по формуле

\[\tilde x \in \left[ {\exp \left( {\bar x \pm {t_\alpha }\frac{s}{{\sqrt n }}} \right)} \right].\]

Учитывая, что при уровне значимости \(\alpha = 0,05\) и \(v = n - 1 = 22\) степенях свободы \(t = 2,074\), то 95% доверительный интервал для медианы давности воспалительно-репаративной реакции в контузионных очагах с наличием зернистых шаров равен

\[\tilde x \in \left[ {\exp \left( {5,598 \pm 2,074 \cdot 0,577/\sqrt {23} } \right)} \right] = \left[ {210;347} \right] ч.\]

Доверительный интервал для значений х логнормальной модели давности ушибов с наличием зернистых шаров в качестве проявления воспалительно-репаративной реакции можно определить опосредованно, используя свойства нормального распределения:

\[x \in \left[ {\exp \left( {\bar x \pm {k_{\alpha ;\gamma ;n}} \cdot s} \right)} \right],\]

где \({k_{\alpha ;\gamma ;n}}\) - допустимый коэффициент для нормального распределения. Величина \({k_{\alpha ;\gamma ;n}}\) зависит от доли γ членов генеральной совокупности, которые должны попасть в доверительный интервал, от вероятности \(1 - \alpha \) того, что они действительно туда попали и от объема выборки n [22,31].

Поскольку для n=23, \(\gamma = 0,90\) и \(\alpha = 0,05\) допустимый коэффициент равен k=2,26, то с 90% надежностью 95% доверительный интервал для значений давности воспалительно-репаративной реакции в очагах ушибов головного мозга с наличием зернистых шаров определяется как

\[x \in \left[ {\exp \left( {5,598 \pm 2,26 \cdot 0,577} \right)} \right] = \left[ {73;996} \right] ч.\]

Доверительные интервалы для значений случайной величины х, характеризующейся каким-либо неизвестным или не подчиняющимся нормальному закону распределением, можно также определить на основе использования неравенства Чебышева, доказанного в теории вероятностей [23]. В терминах статистической совокупности оно имеет следующую трактовку: для любой выборочной совокупности доля значений, попадающих в интервал \(\bar x \pm ks\) будет равна, по крайней мере, \(1 - 1/{k^2}\), где k – любое число, большее 1 [58,60]. Ценность неравенства Чебышева заключается в том, что оно будет верно для любого частотного распределения данных. Однако ценой универсальности данного метода будет довольно значительное снижение точности определения давности моделируемого процесса.

Например, 95% доверительный интервал для значений давности воспалительно-репаративной реакции в очагах ушиба головного мозга с наличием зернистых шаров, рассчитанный с использованием неравенства Чебышева, равен \(x \in \left[ { - 743;1386} \right]\) ч. Учитывая, что случайная величина х не может принимать отрицательные значения по самой природе данных, то полученный результат идентификации давности черепно-мозговой травмы должен быть записан в виде \(x \in \left[ {0;1386} \right]\) ч.

В целом полученные данные позволяют устанавливать доверительные интервалы давности событий при отсутствии какой-либо дополнительной информации о сроках их наступления. Вместе с тем разработанные математические принципы не применимы для дифференциальной диагностики давности событий при наличии определенных версий о возможных сроках их реализации. Это особенно актуально для судебно-медицинских экспертиз по материалам уголовных дел, основным поводом для назначения которых зачастую является необходимость определения возможностей и вероятностей существующих версий о давности юридически значимых событий.

Например, в настоящее время дифференциальная диагностика давности ушибов головного мозга в подобных условиях осуществляется путем выявления каких-либо проявлений эволюции названных повреждений (преимущественно патоморфологических) с последующим исключением тех гипотез, предполагаемые сроки реализации которых выходят за пределы хронологических интервалов наличия или отсутствия выявленных в ходе экспертного исследования диагностических критериев. Однако подобная тактика малоэффективна в тех случаях, когда зарегистрированные диагностические критерии давности ушибов головного мозга могут отмечаться в сроки, предполагаемые сразу несколькими альтернативными следственными версиями.

В общем случае объективное оценивание конкретных версий давности моделируемых процессов подразумевает определение априорных вероятностей каждой из них и последующую переоценку по теореме Байеса.

Пусть n – количество дифференцируемых версий давности \({x_i}\) юридически значимого события, где \(i = 1,2, \ldots ,n\) - порядковый номер каждой версии. Тогда апостериорные вероятности соответствия неизвестной истиной давности значениям, предполагаемым каждой версией, определяются по формуле

\[P({x_i} - \varepsilon < {x_i} < {x_i} + \varepsilon ) = \int\limits_{{x_i} - \varepsilon }^{{x_i} + \varepsilon } {f(x)dx} , (3)\]

где \(P({x_i} - \varepsilon < {x_i} < {x_i} + \varepsilon )\) - априорная вероятность наступления юридически значимого события в промежуток времени \({x_i} \pm \varepsilon \), в котором ε – любая наперед заданная погрешность.

Апостериорные вероятности следует вычислять по формуле

\[{P_i} = \frac{{P({x_i} - \varepsilon < {x_i} < {x_i} + \varepsilon )}}{{\sum\limits_{i = 1}^{i = n} {P({x_i} - \varepsilon < {x_i} < {x_i} + \varepsilon )} }}, (4)\]

где Pi - апостериорная вероятность данной версии события (3).

Указанные данные позволили разработать формулы вычисления априорных вероятностей различных экспертных или следственных версий давности ушибов головного мозга при многократной травме головы:

\[P({x_i} \in {x_i} \pm \varepsilon ) = \exp \left( { - 0,01413725 \cdot ({x_i} - \varepsilon )} \right) - \exp \left( { - 0,01413725 \cdot ({x_i} + \varepsilon )} \right) (5)\]

для признака отсутствия зернистых шаров и астроцитарного глиоза,

\[P({x_i} \in {x_i} \pm \varepsilon ) = \frac{1}{{0,577548751\sqrt {2\pi } }}\int\limits_{{t_i} - \varepsilon }^{{t_i} + \varepsilon } {\exp \left\{ { - \frac{{{{(\ln x - {\rm{5}}{\rm{,59847471}})}^2}}}{{{\rm{2}} \cdot {\rm{0}}{\rm{,57754875}}{{\rm{1}}^{\rm{2}}}}}} \right\}} dx (6)\]

для признака наличия зернистых шаров,

\[P({x_i} \in {x_i} \pm \varepsilon ) = \frac{1}{{1,19373518\sqrt {2\pi } }}\int\limits_{{t_i} - \varepsilon }^{{t_i} + \varepsilon } {\exp \left\{ { - \frac{{{{(\ln x - 4,{\rm{30566755}})}^2}}}{{{\rm{2}} \cdot {{1,19373518}^{\rm{2}}}}}} \right\}} dx\]

для признака наличия фибрина в субарахноидальном кровоизлиянии,

\[P({x_i} \in {x_i} \pm \varepsilon ) = \frac{1}{{0,657629409\sqrt {2\pi } }}\int\limits_{{t_i} - \varepsilon }^{{t_i} + \varepsilon } {\exp \left\{ { - \frac{{{{(\ln x - {\rm{5}}{\rm{,35794491}})}^2}}}{{{\rm{2}} \cdot {{0,657629409}^{\rm{2}}}}}} \right\}} dx\]

для признака наличия мононуклеарной инфильтрации субарахноидального пространства, где \({x_i}\) – давность ушиба согласно определенной версии; ч; ε – окрестность хронологической точки t_i, выбираемая произвольно или в зависимости от погрешности числовых значений сроков давности в рамках представленных следственных версий. При выборе величины ε следует руководствоваться следующим правилом: меньшим по отношению к величине \({x_i}\) значениям ε соответствует большая точность вычислений, но ε не может быть равна 0.

Знание априорных вероятностей версий давности ушибов головного мозга определяет принципиальную возможность их переоценки в каждом экспертном исследовании с вычислением соответствующих апостериорных вероятностей по формуле (4).

Использование предложенных критериев оценки экспертных или следственных версий давности ушибов головного мозга при многократной травме головы можно продемонстрировать на следующем примере.

Согласно следственным данным пострадавшему в различное время до его смерти было нанесено 3 удара по голове. Давность указанных эпизодов травмы головы составляет 24 ч, 168 ч и 480 ч. При судебно-медицинском исследовании трупа потерпевшего обнаружены очаговые ушибы правой лобной и левой височной долей головного мозга. На разрешение судебно-медицинской экспертизы вынесен вопрос о возможности образования обнаруженных ушибов головного мозга в указанные (24 ч, 168 ч и 480 ч) сроки до смерти потерпевшего.

При микроскопическом исследовании фрагментов ушиба правой лобной доли установлено отсутствие зернистых шаров и астроцитарного глиоза. Примем \(\varepsilon = 0,001\) ч.

Отсюда по формуле (5) априорные вероятности дифференцируемых версий давности ушиба правой лобной доли составляют

\[P({x_1} \in {x_1} \pm \varepsilon ) = \exp \left( { - 0,01413725 \cdot (24 - 0,001)} \right) - \exp \left( { - 0,01413725 \cdot (24 + 0,001)} \right) = 2,014 \cdot {10^{ - 5}},\]

\[P({x_2} \in {x_2} \pm \varepsilon ) = \exp \left( { - 0,01413725 \cdot (168 - 0,001)} \right) - \exp \left( { - 0,01413725 \cdot (168 + 0,001)} \right) = 2,630 \cdot {10^{ - 6}},\]

\[P({x_3} \in {x_3} \pm \varepsilon ) = \exp \left( { - 0,01413725 \cdot (480 - 0,001)} \right) - \exp \left( { - 0,01413725 \cdot (480 + 0,001)} \right) = 3,194 \cdot {10^{ - 8}},\]

где \({x_1} = 24\) ч, \({x_2} = 168\) ч и \({x_3} = 480\) ч.

Тогда по формуле (4) апостериорные вероятности дифференцируемых версий давности ушиба правой лобной доли равны

\[{P_1} = \frac{{{\rm{2}}{\rm{,014}} \cdot {\rm{1}}{{\rm{0}}^{{\rm{ - 5}}}}}}{{{\rm{2}}{\rm{,014}} \cdot {\rm{1}}{{\rm{0}}^{{\rm{ - 5}}}}{\rm{ + 2}}{\rm{,630}} \cdot {\rm{1}}{{\rm{0}}^{{\rm{ - 6}}}} + 3,194 \cdot {{10}^{ - 8}}}} = {\rm{0}}{\rm{,883262}},\]

\[{P_2} = \frac{{{\rm{2}}{\rm{,630}} \cdot {\rm{1}}{{\rm{0}}^{{\rm{ - 6}}}}}}{{{\rm{2}}{\rm{,014}} \cdot {\rm{1}}{{\rm{0}}^{{\rm{ - 5}}}}{\rm{ + 2}}{\rm{,630}} \cdot {\rm{1}}{{\rm{0}}^{{\rm{ - 6}}}} + 3,194 \cdot {{10}^{ - 8}}}} = {\rm{0}}{\rm{,115337}},\]

\[{P_3} = \frac{{{\rm{3}}{\rm{,194}} \cdot {\rm{1}}{{\rm{0}}^{{\rm{ - 8}}}}}}{{{\rm{2}}{\rm{,014}} \cdot {\rm{1}}{{\rm{0}}^{{\rm{ - 5}}}}{\rm{ + 2}}{\rm{,630}} \cdot {\rm{1}}{{\rm{0}}^{{\rm{ - 6}}}} + 3,194 \cdot {{10}^{ - 8}}}} = {\rm{0}}{\rm{,001401}}.\]

При микроскопическом исследовании ушиба левой височной доли выявлено наличие зернистых шаров. Поэтому по формуле (6) априорные вероятности дифференцируемых версий давности ушиба левой височной доли составляют

\[P({x_1} \in {x_1} \pm \varepsilon ) = \frac{1}{{0,577548751\sqrt {2\pi } }}\int\limits_{24 - 0,001}^{24 + 0,001} {\exp \left\{ { - \frac{{{{(\ln x - {\rm{5}}{\rm{,59847471}})}^2}}}{{{\rm{2}} \cdot {\rm{0}}{\rm{,57754875}}{{\rm{1}}^{\rm{2}}}}}} \right\}} dx = 8,838 \cdot {10^{ - 9}},\]

\[P({x_2} \in {x_2} \pm \varepsilon ) = \frac{1}{{0,577548751\sqrt {2\pi } }}\int\limits_{168 - 0,001}^{168 + 0,001} {\exp \left\{ { - \frac{{{{(\ln x - {\rm{5}}{\rm{,59847471}})}^2}}}{{{\rm{2}} \cdot {\rm{0}}{\rm{,57754875}}{{\rm{1}}^{\rm{2}}}}}} \right\}} dx = 5,868 \cdot {10^{ - 6}},\]

\[P({x_3} \in {x_3} \pm \varepsilon ) = \frac{1}{{0,577548751\sqrt {2\pi } }}\int\limits_{480 - 0,001}^{480 + 0,001} {\exp \left\{ { - \frac{{{{(\ln x - {\rm{5}}{\rm{,59847471}})}^2}}}{{{\rm{2}} \cdot {\rm{0}}{\rm{,57754875}}{{\rm{1}}^{\rm{2}}}}}} \right\}} dx = 1,752 \cdot {10^{ - 6}}.\]

Согласно (4) апостериорные вероятности дифференцируемых версий давности ушиба левой височной доли равны

\[{P_1} = \frac{{{\rm{8}}{\rm{,838}} \cdot {\rm{1}}{{\rm{0}}^{{\rm{ - 9}}}}}}{{{\rm{8}}{\rm{,838}} \cdot {\rm{1}}{{\rm{0}}^{{\rm{ - 9}}}}{\rm{ + 5}}{\rm{,868}} \cdot {\rm{1}}{{\rm{0}}^{{\rm{ - 6}}}} + 1,752 \cdot {{10}^{ - 6}}}} = {\rm{0}}{\rm{,001158}},\]

\[{P_2} = \frac{{{\rm{5}}{\rm{,868}} \cdot {\rm{1}}{{\rm{0}}^{{\rm{ - 6}}}}}}{{{\rm{8}}{\rm{,838}} \cdot {\rm{1}}{{\rm{0}}^{{\rm{ - 9}}}}{\rm{ + 5}}{\rm{,868}} \cdot {\rm{1}}{{\rm{0}}^{{\rm{ - 6}}}} + 1,752 \cdot {{10}^{ - 6}}}} = {\rm{0}}{\rm{,769132}},\]

\[{P_3} = \frac{{{\rm{1}}{\rm{,752}} \cdot {\rm{1}}{{\rm{0}}^{{\rm{ - 6}}}}}}{{{\rm{8}}{\rm{,838}} \cdot {\rm{1}}{{\rm{0}}^{{\rm{ - 9}}}}{\rm{ + 5}}{\rm{,868}} \cdot {\rm{1}}{{\rm{0}}^{{\rm{ - 6}}}} + 1,752 \cdot {{10}^{ - 6}}}} = {\rm{0}}{\rm{,229710}}.\]

Таким образом, давность ушиба правой лобной доли головного мозга составляет 24 ч (с вероятностью 88,3%), ушиба левой височной доли – 168 ч (с вероятностью 76,9%).

Изложенные принципы математического описания качественной кинетики патоморфологических процессов были многократно использованы авторами при моделировании хронологии развития нетравматических внутрижелудочковых кровоизлияний у недоношенных новорожденных [51], воспалительно-репаративной реакции при закрытой и открытой непроникающей черепно-мозговой травме [52,63], инфарктов и вторичных внутристволовых кровоизлияний при травматическом сдавлении головного мозга [53,56,65]. Результатом явилось создание и внедрение в экспертную практику способов определения продолжительности внеутробной жизни недоношенных новорожденных, давности черепно-мозговой травмы и продолжительности травматического сдавления головного мозга.

Таким образом, моделирование распределений давности изучаемого процесса с наличием одного или группы различных его проявлений на основе использования эмпирических статистических данных является апробированным методом математического описания качественной кинетики физиологических, патоморфологических и постмортальных процессов при реконструкции их давности. Указанный подход позволяет в количественной вероятностной форме устанавливать давность и продолжительность событий, вследствие чего должен являться обязательным компонентом любых исследований, посвященных созданию способов судебно-медицинского установления давности физиологических, патоморфологических и постмортальных процессов. Метод целесообразно также использовать для определения давности юридически значимых событий в условиях наличия дополнительной следственной информации о предполагаемых сроках их наступления.

Приведенные математические принципы не исключают возможности разработки альтернативных аналитических методов вероятностной судебно-медицинской реконструкции давности юридически значимых событий.

Читать далее раздел "4.3. Реконструкция механизма травмы"⇒