Вы здесь
3.4. Интервальное оценивание достоверности судебно-медицинской идентификации
По своей сути ключевые критерии достоверности категоричной судебно-медицинской идентификации представляют собой относительные частотные показатели. Так, чувствительность представляет собой долю истинно положительных результатов идентификации в совокупности объектов с наличием идентифицируемого состояния, специфичность – долю истинно отрицательных результатов в совокупности объектов с отсутствием идентифицируемого состояния. Прогностическая ценность положительной идентификации представляет собой долю истинно положительных результатов в совокупности всех положительных результатов идентификации, прогностическая ценность отрицательной идентификации – долю истинно отрицательных результатов в совокупности всех отрицательных результатов идентификации.
Ввиду невозможности исследования разработчиками диагностических технологий генеральных совокупностей объектов все перечисленные критерии достоверности категоричной идентификации определяются с использованием тестовых выборок ограниченного объема. Поэтому простое определение долей указанных результатов дает лишь ориентировочное представление о достоверности идентификации. В этой связи для обоснованного суждения о достоверности категоричной идентификации необходимо вычисление интервальных оценок каждого ключевого критерия последней. Данная рекомендация согласуется с общей тенденцией к расширению показаний к применению доверительных интервалов в биомедицинских исследованиях вплоть до замены ими обычных статистических критериев [150].
Доверительные интервалы для показателей чувствительности и специфичности категоричной идентификации могут быть определены различными способами [41,103,116,146]. Одним из наиболее простых и строгих из них является вычисление точных доверительных границ биномиально распределенной генеральной совокупности, который и будет изложен ниже.
Следует подчеркнуть, что случайная дискретная величина подчиняется биномиальному распределению, только если выполняются следующие условия, называемые свойствами независимых испытаний Бернулли [22]:
- Каждое отдельное наблюдение имеет ровно два возможных взаимно исключающих исхода.
- Вероятность исхода одна и та же для любого наблюдения.
- Все наблюдения независимы друг от друга.
При соответствии эмпирических данных указанным условиям точные доверительные границы биномиально распределенной генеральной совокупности определяются по формулам:
${\pi _B} = \frac{{(x + 1) \cdot F}}{{n - x + (x + 1) \cdot F}}$ при ${F_{\{ {v_1} = 2 \cdot (x + 1),{v_2} = 2 \cdot (n - x)\} }},$
${\pi _H} = \frac{x}{{x + (n - x + 1) \cdot F}}$ при ${F_{\{ {v_1} = 2 \cdot (n - x + 1),{v_2} = 2x\} ,}}$
где ${\pi _B}$ и ${\pi _H}$ - соответственно верхняя и нижняя односторонние доверительные границы для выборочного относительного частотного показателя р; х – число положительных выборочных наблюдений); n – объем выборки; F - значение F-распределения для выбранной доверительной вероятности в зависимости от обоих чисел степеней свободы [31].
Например, для показателя чувствительности идентификации отека головного мозга по его массе приведенные формулы при 95% уровне надежности принимают вид:
${\pi _B} = \frac{{(a + 1) \cdot F}}{{(a + c) - a + (a + 1) \cdot F}} \approx 0,327$ при ${F_{\{ a = 0,025,{v_1} = 2 \cdot (a + 1),{v_2} = 2 \cdot (a + c - a)\} }} = {\rm{1}}{\rm{,735}}$,
${\pi _H} = \frac{a}{{a + (a + c - a + 1) \cdot F}} \approx 0,115$ при ${F_{\{ a = 0,025,{v_1} = 2 \cdot (a + c - a + 1),{v_2} = 2a\} }} = {\rm{1}}{\rm{,967}}$,
где а – количество истинно положительных, а с – количество ложноотрицательных результатов идентификации тестовой выборки объектов. Остальные интервальные оценки чувствительности и специфичности приведены в таблице 7.
Точные доверительные интервалы асимметричны относительно выборочной оценки р относительного частотного показателя. Симметричными доверительные границы являются только при p=0,5.
Особый случай при расчетах доверительных оценок составляют нуль-событие и полное событие. Точную верхнюю интервальную оценку доли генеральной совокупности при (нуль-событие) можно также вычислить с помощью выражения ${\pi _B} = 1 - \sqrt[n]{a}$. Для p=1 (полное событие) нижняя граница определяется формулой ${\pi _H} = \sqrt[n]{a}$ [31].
Таблица 7
Точечные и 95% двусторонние интервальные оценки критериев достоверности идентификации отека головного мозга
| Критерий |
Мужчины | Женщины | ||||
|---|---|---|---|---|---|---|
| α | 0,010 | 0,049 | 0,137 | 0,008 | 0,667 | 0,208 |
| β | 0,673 | 0,794 | 0,885 | 0,384 | 0,062 | 0,882 |
| 1-β | 0,115 | 0,206 | 0,327 | 0,118 | 0,333 | 0,616 |
| 1-α | 0,863 | 0,951 | 0,990 | 0,792 | 0,938 | 0,992 |
| γ | 0,022 | 0,192 | 0,591 | 0,008 | 0,158 | 0,699 |
| δ | 0,398 | 0,455 | 0,513 | 0,260 | 0,416 | 0,539 |
| 1-γ | 0,409 | 0,808 | 0,978 | 0,301 | 0,842 | 0,992 |
| 1-δ | 0,487 | 0,545 | 0,602 | 0,461 | 0,584 | 0,740 |
Таким образом, определение интервальных оценок чувствительности и специфичности должно стать обязательным компонентом любой программы тестирования достоверности способов категоричной судебно-медицинской идентификации. К сожалению, определение интервальных оценок для наиболее значимого критерия достоверности – прогностической ценности положительного результата идентификации является затруднительным. Это объясняется тем, что простое вычисление доверительных границ для указанного критерия, принимая за выборочную относительную величину долю истинно положительных результатов в совокупности всех положительных результатов идентификации, не имеет смысла, поскольку как уже было показано, сама точечная оценка сильно зависит от распространенности идентифицируемого состояния С. Аналогично дело обстоит и с другими ключевыми критериями достоверности идентификации, зависящими от распространенности идентифицируемого состояния С.
В этой связи весьма актуальной является проблема определения доверительных границ для критериев достоверности γ, δ, ε и ζ. Трудность поставленной задачи определяется тем, что в определяющие тождества данных критериев входят точечные оценки сразу двух параметров одновременно: α и β. Вследствие этого в судебно-медицинской литературе даже высказывалось мнение о невозможности общего решения подобных проблем и предлагались отдельные решения ее частных случаев [60].
Изложенное позволило авторам предложить метод определения доверительных границ для каждого из указанных критериев достоверности идентификации, суть которого сводится к следующему:
- При выбранном уровне значимости вычисляют интервальные оценки показателей α и β.
- Определяют доверительные границы для критериев γ, δ, ε и ζ при удвоенном уровне значимости, используя вместо точечных все возможные комбинации интервальных оценок α и β.
- Из четырех возможных комбинаций выбирают оценки с наименьшими нижними и наибольшими верхними доверительными границами.
Выведем на основе предложенного метода формулы доверительных границ для показателей γ и ε.
Пусть доверительные границы для α и β, входящих в определяющее тождество γ, при уровне значимости α составляют \(\alpha = \left[ {{\alpha _{\min }};{\alpha _{\max }}} \right]\) и $\beta = \left[ {{\beta _{\min }};{\beta _{\max }}} \right]$.
Тогда множество G интервальных оценок γ состоит из 4 элементов, представляющих собой различные комбинации наибольших и наименьших доверительных границ α и β:
\(G = \left\{ {\frac{{{\alpha _{\min }}}}{{{\alpha _{\min }} + 1 - {\beta _{\min }}}},\frac{{{\alpha _{\min }}}}{{{\alpha _{\min }} + 1 - {\beta _{\max }}}},\frac{{{\alpha _{\max }}}}{{{\alpha _{\max }} + 1 - {\beta _{\min }}}},\frac{{{\alpha _{\max }}}}{{{\alpha _{\max }} + 1 - {\beta _{\max }}}}} \right\}\).
Количество анализируемых комбинаций интервальных оценок α и β можно сократить путем их частичного упорядочивания с помощью отношения <.
Нетрудно доказать, что в частично упорядоченном на основе указанного строгого неравенства множестве G элемент, содержащий оценки \({\alpha _{\min }}\) и \({\beta _{\min }}\), является наименьшим, а элемент, содержащий оценки \({\alpha _{\max }}\) и \({\beta _{\max }}\), - наибольшим:
\(\inf \left\{ G \right\} = \frac{{{\alpha _{\min }}}}{{{\alpha _{\min }} + 1 - {\beta _{\min }}}}\),
\(\sup \left\{ G \right\} = \frac{{{\alpha _{\max }}}}{{{\alpha _{\max }} + 1 - {\beta _{\max }}}}\).
Соответствующие пределы для γ равны
\(\mathop {\lim }\limits_{\scriptstyle\alpha \to 0\atop\scriptstyle\beta \to 0} \frac{\alpha }{{\alpha + 1 - \beta }} = 0\), \(\mathop {\lim }\limits_{\scriptstyle\alpha \to 1\atop\scriptstyle\beta \to 1} \frac{\alpha }{{\alpha + 1 - \beta }} = 1\).
Элементы же
\[\frac{{{\alpha _{\min }}}}{{{\alpha _{\min }} + 1 - {\beta _{\max }}}} и \frac{{{\alpha _{\max }}}}{{{\alpha _{\max }} + 1 - {\beta _{\min }}}}\]
могут характеризоваться всеми возможными взаимными отношениями: <, =, >.
Таким образом, наименьшей нижняя доверительная граница для γ будет при комбинации \(\left\{ {{\alpha _{\min }},{\beta _{\min }}} \right\}\), а наибольшей – при комбинации \(\left\{ {{\alpha _{\max }},{\beta _{\max }}} \right\}\).
Отсюда интервальные оценки для γ с надежностью не менее \(1 - 2a\) определяются как \(\gamma = \left[ {{\gamma _{\min }};{\gamma _{\max }}} \right]\),
где \({\gamma _{\min }} = \frac{{{\alpha _{\min }}}}{{{\alpha _{\min }} + 1 - {\beta _{\min }}}}\), \({\gamma _{\max }} = \frac{{{\alpha _{\max }}}}{{{\alpha _{\max }} + 1 - {\beta _{\max }}}}\).
Интервальные оценки γ легко модифицировать в соответствующие оценки ε при уровне надежности не менее \(1 - 2a\):
\(\varepsilon = \left[ {{\varepsilon _{\min }};{\varepsilon _{\max }}} \right]\), где \({\varepsilon _{\min }} = \frac{{P(\bar C) \cdot {\alpha _{\min }}}}{{P(\bar C) \cdot {\alpha _{\min }} + P(C) \cdot (1 - {\beta _{\min }})}}\), \({\varepsilon _{\max }} = \frac{{P(\bar C) \cdot {\alpha _{\max }}}}{{P(\bar C) \cdot {\alpha _{\max }} + P(C) \cdot (1 - {\beta _{\max }})}}\).
Рассмотрим теперь вывод формул доверительных границ для показателей δ и ζ.
По аналогии с γ множество D интервальных оценок δ также состоит из 4 элементов, представляющих собой различные комбинации наибольших и наименьших доверительных границ α и β:
\[D = \left\{ {\frac{{{\beta _{\min }}}}{{{\beta _{\min }} + 1 - {\alpha _{\min }}}},\frac{{{\beta _{\min }}}}{{{\beta _{\min }} + 1 - {\alpha _{\max }}}},\frac{{{\beta _{\max }}}}{{{\beta _{\max }} + 1 - {\alpha _{\min }}}},\frac{{{\beta _{\max }}}}{{{\beta _{\max }} + 1 - {\alpha _{\max }}}}} \right\}\].
Сократим количество анализируемых комбинаций интервальных оценок α и β путем их частичного упорядочивания с помощью отношения <.
Тогда в частично упорядоченном на основе указанного строгого неравенства множестве D элемент, содержащий оценки \({\alpha _{\min }}\) и \({\beta _{\min }}\), является наименьшим, а элемент, содержащий оценки \({\alpha _{\max }}\) и \({\beta _{\max }}\), - наибольшим:
\(\inf \left\{ D \right\} = \frac{{{\beta _{\min }}}}{{{\beta _{\min }} + 1 - {\alpha _{\min }}}}\), \(\sup \left\{ D \right\} = \frac{{{\beta _{\max }}}}{{{\beta _{\max }} + 1 - {\alpha _{\max }}}}\).
Определим соответствующие пределы для δ:
\(\mathop {\lim }\limits_{\scriptstyle\alpha \to 0\atop\scriptstyle\beta \to 0} \frac{\beta }{{\beta + 1 - \alpha }} = 0\) и \(\mathop {\lim }\limits_{\scriptstyle\alpha \to 1\atop\scriptstyle\beta \to 1} \frac{\beta }{{\beta + 1 - \alpha }} = 1\).
Отсюда интервальные оценки для δ с надежностью не менее \(1 - 2a\) определяются как
\(\delta = \left[ {{\delta _{\min }};{\delta _{\max }}} \right]\), где
\[{\delta _{\min }} = \frac{{{\beta _{\min }}}}{{{\beta _{\min }} + 1 - {\alpha _{\min }}}},\]
\[{\delta _{\max }} = \frac{{{\beta _{\max }}}}{{{\beta _{\max }} + 1 - {\alpha _{\max }}}}.\]
В свою очередь, интервальные оценки ζ с надежностью не менее \(1 - 2a\) принадлежат промежутку
\(\zeta = \left[ {{\zeta _{\min }};{\zeta _{\max }}} \right]\), где
\[{\zeta _{\min }} = \frac{{P(C) \cdot {\beta _{\min }}}}{{P(C) \cdot {\beta _{\min }} + P(\bar C) \cdot (1 - {\alpha _{\min }})}},\]
\[{\zeta _{\max }} = \frac{{P(C) \cdot {\beta _{\max }}}}{{P(C) \cdot {\beta _{\max }} + P(\bar C) \cdot (1 - {\alpha _{\max }})}}.\]
Используя интервальные оценки γ, δ, ε и ζ, с надежностью не менее \(1 - 2a\) легко определяются доверительные границы значений прогностической ценности результатов идентификации: \(1 - \gamma = \left[ {1 - {\gamma _{\max }};1 - {\gamma _{\min }}} \right]\), \(1 - \delta = \left[ {1 - {\delta _{\max }};1 - {\delta _{\min }}} \right]\),
\(1 - \varepsilon = \left[ {1 - {\varepsilon _{\max }};1 - {\varepsilon _{\min }}} \right]\) при \(P(C) = \left[ {0;1} \right]\),
\(1 - \zeta = \left[ {1 - {\zeta _{\max }};1 - {\zeta _{\min }}} \right]\) при \(P(C) = \left[ {0;1} \right]\).
В качестве примера использования полученных формул продолжим определение интервальных оценок критериев достоверности идентификации отека головного мозга по его массе.
Как было показано, точечные оценки чувствительности и специфичности идентификации отека мозга у мужчин равны \(1 - \beta = 0,206\) и \(1 - \alpha = 0,651\).
Отсюда аналогичные оценки α и β составляют \(\alpha = 0,049\) и \(\beta = 0,794\).
Для дальнейших расчетов потребуется определение 97,5% интервальных оценок α и β.
С учетом округления соответствующие точные биномиальные оценки равны \(\alpha = \left[ {0,008;0,151} \right]\) и \(\beta = \left[ {0,656;0,895} \right]\).
Тогда интервальные оценки γ с учетом округления и надежностью не менее 95% определяются как \(\gamma = \left[ {{\gamma _{\min }};{\gamma _{\max }}} \right]\), где
\[{\gamma _{\min }} = \frac{{0,008}}{{0,008 + 1 - 0,656}} = 0,022,\]
\[{\gamma _{\max }} = \frac{{0,151}}{{0,151 + 1 - 0,895}} = 0,591.\]
Поэтому интервальные оценки прогностической ценности положительного результата идентификации равны \(1 - \gamma = \left[ {1 - 0,591;1 - 0,022} \right] = \left[ {0,409;0,978} \right]\).
Интервальные оценки остальных критериев идентификации отека головного мозга у мужчин, а также у женщин приведены в таблице 7.
При необходимости интервальные оценки прогностической ценности положительного и отрицательного результатов идентификации могут быть вычислены и с учетом распространенности идентифицируемого состояния С в совокупности объектов идентификации. Ввиду непрерывности множества указанных оценок результаты их вычисления целесообразно представлять в форме номограмм. Например, номограмма определения точечных и интервальных оценок прогностической ценности результатов положительной идентификации отека головного мозга у мужчин в зависимости от априорной вероятности данного состояния приведена на рисунке 5.
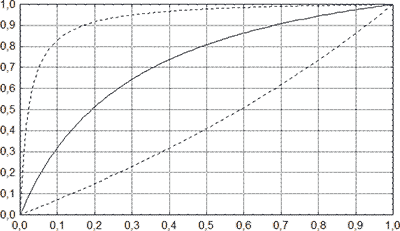
Рис. 5. Номограмма определения точечных и 95% интервальных оценок прогностической ценности положительной идентификации при различной распространенности идентифицируемого состояния. По оси абсцисс – доля объектов с наличием состояния С; по оси ординат – прогностическая ценность положительной идентификации. Сплошной линией показаны точечные, пунктирными линиями – 95% двусторонние интервальные оценки. Чувствительность, специфичность и отношение правдоподобия идентификации фиксированы и равны 0,206; 0,951 и 4,2 соответственно.
Таким образом, на современном этапе развития судебной медицины и биомедицины в целом разработка любых диагностических или скрининговых технологий должна включать обязательное точечное и интервальное оценивание ключевых критериев достоверности. Наличие подобного тестирования является необходимым условием для внедрения новой диагностической технологии в медицинскую практику. В этой связи в судебной медицине помимо создания новых технологий актуальными также представляются исследования достоверности диагностических методик и морфологических диагностических признаков, ставших известными до распространения принципов доказательной медицины и уже укоренившихся в практической экспертной деятельности. Изложенные принципы подразумевают внесение соответствующих дополнений в систему подготовки судебно-медицинских экспертов.
Читать далее раздел "3.5. Достоверность полиномиальной судебно-медицинской идентификации"⇒

