Вы здесь
3.3. Критерии достоверности судебно-медицинской идентификации
На практике результаты судебно-медицинской идентификации определенного состояния С часто формулируются в форме категоричных экспертных суждений. Алгоритм применения каждой подобной диагностической технологии обычно включает регистрацию наличия или отсутствия какого-либо признака $x \in X$. Элементы зафиксированного множества Х признаков обладают различной диагностической значимостью. В этой связи в отношении каждого признака, факт наличия которого используется в качестве посылки для формулирования заключения о положительной идентификации состояния С, принципиально важно знать характеристики достоверности диагностики.
Понятие достоверности в судебной медицине, как и в биомедицине в целом, является многозначным и включает в себя комплекс критериев оценки результатов диагностических и скрининговых тестов. К числу основных компонентов данного комплекса относятся следующие характеристики: чувствительность (sensitivity), специфичность (specificity), прогностическая ценность положительного (positive predictive value) и отрицательного (negative predictive value) результатов, индекс точности (accuracy) и отношение правдоподобия положительного результата (likelihood ratio of a positive test) [26,132,148]. Каждый критерий представляет собой определенный вероятностный показатель, определяемый статистически.
Основная идея статистического оценивания достоверности заключается в том, что при судебно-медицинской идентификации состояния С возможны 4 типа результатов: истинно положительные, ложноположительные, ложноотрицательные и истинно отрицательные. С учетом этого ключевые показатели достоверности идентификации можно охарактеризовать следующим образом.
Допустим, необходимо оценить достоверность признака $x \in X$, предназначенного для идентификации состояния С. Обозначая обладание произвольным объектом z признаком х и свойством С одноместными предикатами X(z) и C(z) соответственно, правило идентификации состояния С и противоположного ему состояния $\bar C$ на языке логики предикатов можно описать формулами $\forall z\left\{ {X(z) \to C(z)} \right\}$; $\forall z\left\{ {\neg X(z) \to \neg C(z)} \right\}$.
Тогда для оценки достоверности идентификации на этапе разработки диагностической медицинской технологии необходимо исследовать наличие признака х в совокупности объектов объемом n с заведомо известным наличием или отсутствием состояния С.
Пусть a, b, c, d - количество зарегистрированных истинно положительных, ложноположительных, ложноотрицательных и истинно отрицательных результатов идентификации состояния С соответственно: n=a+b+c+d. Отсюда общее количество положительных результатов идентификации равно a+b, а отрицательных – c+d. Количество объектов с состоянием С равно a+c, а с альтернативным состоянием $\bar C$ - b+d (табл. 5).
Таблица 5 Возможные результаты судебно-медицинской идентификации
| Результат теста | Наличие состояния С | |
| $C:a + c$ | $\bar C:b + d$ | |
| Положительный α+b α+b-β |
Истинно положительный α 1-β |
Ложноположительный b α |
| Отрицательный c+d β+1-α |
Ложноотрицательный c β |
Истинно отрицательный d 1-α |
В этом случае критерии достоверности категоричной идентификации определяются следующими формулами:
чувствительность - ${a \over {a + c}}$;
специфичность - ${d \over {b + d}}$;
прогностическая ценность положительного результата - ${a \over {a + b}}$;
прогностическая ценность отрицательного результата - ${d \over {c + d}}$;
индекс точности - ${{a + d} \over {a + b + c + d}}$;
отношение правдоподобия положительного результата - ${{a(b + d)} \over {b(a + c)}}$.
Рассмотрим изложенные принципы оценивания достоверности судебно-медицинской идентификации на следующем примере.
Отек головного мозга относится к наиболее сложным для экспертной оценки патологическим проявлениям, отличаясь изменением объемных соотношений полости черепа и его содержимого [59]. В этой связи авторами было выполнено исследование возрастной динамики объемов нелабильных внутричерепных структур, а также определена достоверность использования объемно-весовых показателей головного мозга для диагностики его отека [59,60].
В ходе проведенного исследования были получены линейные регрессионные модели возрастной динамики объема и массы головного мозга у мужчин и женщин и доказана возможность использования показателя массы для диагностики отека головного мозга. В частности, реализация разработанного способа диагностики достигается путем измерения массы головного мозга с последующим сравнением полученного результата со значениями возрастной нормы. Идентификация отека головного мозга считается положительной в случае превышения массы мозга верхней 95% односторонней доверительной границы для возрастной нормы. В качестве отрицательных рассматриваются результаты, значения массы головного мозга которых не выходят за пределы указанного доверительного интервала.
Для определения достоверности изложенного способа идентификации отека головного мозга было произведено измерение массы мозга в двух группах мужчин и женщин: с наличием отека головного мозга и без такового.
Группа наблюдений с наличием идентифицируемого состояния была представлена 63 трупами лиц мужского и 15 трупами лиц женского пола, погибших в стационаре от травматического сдавления и отека мозга. Морфологический субстрат сдавления в 56 (71,8%) случаях был представлен односторонними, а в 19 (24,4%) случаях – двусторонними супратенториальными субдуральными гематомами, в 3 (3,8%) случаях – изолированными эпидуральными гематомами. В 3 (3,8%) наблюдениях субдуральные гематомы сочетались с эпидуральными кровоизлияниями, в 64 (82,1%) случаях - с очаговыми ушибами головного мозга. Во всех наблюдениях тестовой выборки имелся характерный для сдавления и дислокации головного мозга комплекс клинических и морфологических проявлений с наличием вторичных внутристволовых кровоизлияний.
Наблюдения с отсутствием идентифицируемого состояния были представлены трупами 61 мужчины и 32 женщин, умерших от различных причин в возрасте от 18 до 92 лет. В данную группу не включались лица с наличием травматических или каких-либо других патологических изменений черепа, вне – и внутричерепных образований, кроме атеросклероза артерий головного мозга при отсутствии его инфарктов и внутримозговых кровоизлияний любого объема и сроков организации. Для исключения возможного влияния на объем головного мозга каких-либо медицинских вмешательств (инфузионная терапия, реанимационные мероприятия) в исследуемые группы также не включались лица, смерть которых наступила в стационаре.
Относительная погрешность определения массы головного мозга в обеих группах не превышала 1%. Результаты оценивания достоверности диагностики отека головного мозга по его массе приведены в таблице 6.
Таблица 6 Результаты оценки достоверности идентификации отека головного мозга по его массе
| Результат идентификации | Мужчины | Женщины | ||
| С | $\bar C$ | С | $\bar C$ | |
| Положительный | 13 | 3 | 5 | 2 |
| Отрицательный | 50 | 58 | 10 | 30 |
Согласно представленным табличным данным чувствительность диагностики отека головного мозга по его массе у мужчин равна 20,6%, специфичность – 95,1%, прогностическая ценность положительного результата идентификации – 81,3%, прогностическая ценность отрицательного результата – 53,7%, индекс точности – 57,3%, отношение правдоподобия положительной идентификации – 4,2. У женщин аналогичные показатели составили: чувствительность – 33,3%, специфичность – 93,8%, прогностическая ценность положительного результата – 71,4%, прогностическая ценность отрицательного результата – 75,0%, индекс точности – 74,5%, отношение правдоподобия – 5,3.
Приведенные показатели чувствительности и специфичности в отношении мужчин означают, что указанный метод правильно идентифицирует 1 из 5 случаев отека головного мозга, правильно исключает 95% случаев с отсутствием отека головного мозга. Положительный результат идентификации в 81% случаев свидетельствует о наличии отека мозга, отрицательный результат идентификации показывает, что вероятность отсутствия отека мозга составляет 54%. Индекс точности означает, что правильная диагностика отека головного мозга или отсутствия таковых имеет место в 57% случаев применения данного метода. Отношение правдоподобия показывает, что положительный результат идентификации в 4,2 раза более вероятен у мужчин с наличием отека головного мозга, чем у таковых с отсутствием указанного состояния. У женщин интерпретация критериев достоверности идентификации сдавления и отека головного мозга аналогична.
Изложенный пример демонстрирует, что любой диагностический метод может быть недостоверен, если хотя бы некоторые из его ключевых характеристик слишком низкие. Так, ввиду почти 80% вероятности ложноотрицательного результата идентификации сравнение массы головного мозга с возрастной нормой больше вводит судебно-медицинских экспертов в заблуждение, нежели помогает диагностике отека мозга.
Важно подчеркнуть, что чувствительность, специфичность и отношение правдоподобия отражают лишь достоверность идентификации в целом, ничего не говоря об интерпретации результатов идентификации состояний С или $\bar C$ у отдельного объекта. Поэтому для практики более значимыми являются показатели прогностической ценности положительного и отрицательного результатов идентификации, а также индекс точности. Первые два из указанных критериев называются также посттестовой вероятностью положительного и отрицательного результатов идентификации соответственно и являются наиболее значимыми, поскольку характеризуют вероятность наличия состояния С у объекта, при исследовании которого зарегистрирован признак $x \in X$ и вероятность отсутствия С (т.е. наличия состояния $\bar C$) у объекта, при исследовании которого признак $x \in X$ не зарегистрирован.
Однако существенным недостатком показателей прогностической ценности результатов идентификации и индекса точности является их зависимость от распространенности идентифицируемого состояния С в популяции. Наличие данной зависимости объясняется тем, что в определяющие тождества указанных критериев достоверности входят некоторые частотные показатели обоих идентифицируемых состояний С и $\bar C$ одновременно. В отличие от данных критериев, подобное вхождение не имеет места в тождествах, определяющих чувствительность и специфичность, вследствие чего последние не зависят от распространенности состояния С.
Так, в приведенном примере доли трупов мужчин с наличием и отсутствием отека головного мозга были практически равны (50,8% и 49,2% соответственно). Однако при других соотношениях объектов с наличием или отсутствием идентифицируемого состояния значения показателей прогностической ценности и индекса точности при тех же значениях чувствительности и специфичности идентификации были бы другими (рис. 4). Вследствие указанной зависимости в общем случае любое смещение соотношения априорных частот состояний С или $\bar C$ в совокупности идентифицируемых объектов от величины, использованной разработчиками способа идентификации при оценивании его достоверности, всегда сопровождается отклонением показателей прогностической ценности и индекса точности от их расчетных значений.
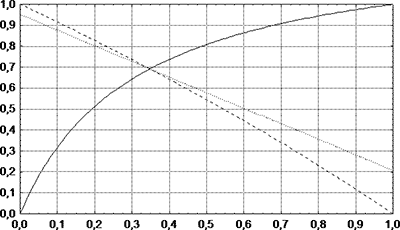
Рис. 4. Зависимость показателей достоверности идентификации от распространенности идентифицируемого состояния. По оси абсцисс – доля объектов с наличием состояния С; по оси ординат – достоверность идентификации. Сплошной линией показана прогностическая ценность положительного результата идентификации, пунктирной – прогностическая ценность отрицательного результата идентификации, точечной – индекс точности. Чувствительность, специфичность и отношение правдоподобия идентификации фиксированы и равны 0,206; 0,951 и 4,2 соответственно.
Данная проблема имеет место и в клинической медицине, вследствие чего практические врачи совершенно правильно с недоверием относятся к характеристикам диагностических и скрининговых тестов, заявленным их разработчиками [26].
Изложенное позволило нам предложить альтернативные критерии прогностической ценности категоричных диагностических результатов, учитывающие распространенность идентифицируемого состояния в совокупности объектов идентификации.
Перед рассмотрением указанных критериев введем понятия априорных вероятностей ложноположительной и ложноотрицательной идентификации состояния С. По сложившейся в математической статистике традиции обозначим указанные вероятности буквами α и β:
$\alpha = {b \over {b + d}}$, $\beta = {c \over {a + c}}$.
Обозначим также буквами Γ и Δ общепринятые в биомедицине прогностические вероятности ложноположительной и ложноотрицательной идентификации С:
$\Gamma = 1 - {a \over {a + b}} = {b \over {a + b}}$, $\Delta = 1 - {d \over {c + d}} = {c \over {c + d}}$. (1)
Благодаря указанным понятиям и обозначениям можно формализовать названия ключевых критериев достоверности идентификации: чувствительность – 1-β, специфичность – 1-α, прогностическая ценность положительного результата - 1-Γ, прогностическая ценность отрицательного результата – 1-Δ.
Альтернативные критерии достоверности представляют собой апостериорные вероятности ложноположительной и ложноотрицательной идентификации, обозначенные нами буквами γ и δ:
$\gamma = {\alpha \over {\alpha + 1 - \beta }}$, $\delta = {\beta \over {\beta + 1 - \alpha }}$.
Связь показателей γ и δ с традиционными показателями Γ и Δ характеризует следующая теорема.
Теорема достоверности идентификации. При оценивании достоверности любых диагностических и скрининговых технологий апостериорные вероятности ложноположительной и ложноотрицательной идентификации состояния С эквивалентны прогностическим вероятностям указанных ошибок тогда и только тогда, когда количество объектов с наличием состояния С в тестовой выборке равно количеству объектов с отсутствием данного состояния:
$\left\{ {a + c = b + d} \right\} \to \left\{ {\gamma = \Gamma \wedge \delta = \Delta } \right\}$.
Приведем доказательство данного утверждения.
По определению
$\eqalign{
& \gamma = {\alpha \over {\alpha + 1 - \beta }} = {b \over {b + d}} \cdot {1 \over {{b \over {b + d}} + 1 - {c \over {a + c}}}} = {b \over {(b + d) \cdot \left( {{b \over {b + d}} + 1 - {c \over {a + c}}} \right)}} = \cr
& = {b \over {b + (b + d) - {{c(b + d)} \over {a + c}}}} = {b \over {2b + d - {{c(b + d)} \over {a + c}}}}. \cr} $
Учитывая (1), $\gamma \equiv \Gamma $, если выполняется равенство
${b \over {2b + d - {{c(b + d)} \over {a + c}}}} = {b \over {a + b}}$. (2)
Из выражения (2) путем ряда эквивалентных преобразований
$2b + d - {{c(b + d)} \over {a + c}} = a + b$, $b + d - {{c(b + d)} \over {a + c}} - a = 0$,
$b(a + c) + d(a + c) - c(b + d) - a(a + c) = 0$,
$ab + bc + ad + cd - bc - cd - {a^2} - ac = 0$,
$ab + ad - {a^2} - ac = 0$, $b + d - a - c = 0$
Получаем $a + c = b + d$. (3)
Таким образом, (2) выполняется, если выполняется (3).
Докажем теперь эквивалентность $\delta \equiv \Delta $.
По определению
$\eqalign{
& \delta = {\beta \over {\beta + 1 - \alpha }} = {c \over {a + c}} \cdot {1 \over {{c \over {a + c}} + 1 - {b \over {b + d}}}} = {c \over {(a + c) \cdot \left( {{c \over {a + c}} + 1 - {b \over {b + d}}} \right)}} = \cr
& = {c \over {c + (a + c) - {{b(a + c)} \over {b + d}}}} = {c \over {2c + a - {{b(a + c)} \over {b + d}}}}. \cr} $.
Ввиду (1) $\delta \equiv \Delta $, если выполняется равенство ${c \over {2c + a - {{b(a + c)} \over {b + d}}}} = {c \over {c + d}}$. (4)
Из выражения (4) путем ряда аналогичных преобразований получаем (3). Таким образом, равенство (4) выполняется, если выполняется условие (3). Теорема доказана.
С помощью предложенных понятий показатели прогностической ценности положительного и отрицательного результатов формульно характеризуются как $1 - \gamma $ и $1 - \delta $. Указанные характеристики постоянны и не зависят от распространенности состояния С в совокупности идентифицируемых объектов. Тем не менее, для определения показателей прогностической ценности идентификации на практике необходимы иные критерии, учитывающие априорную распространенность С.
Пусть P(C) - априорная вероятность (распространенность) состояния С, а $P(\bar C)$ - аналогичная вероятность противоположного состояния $\bar C$ . В этом случае полная группа возможных результатов идентификации С формализуется записью $P(\bar C) \cdot \alpha + P(\bar C) \cdot (1 - \alpha ) + P(C) \cdot \beta + P(C) \cdot (1 - \beta ) = 1$.
Тогда апостериорные вероятности ложноположительной (ε) и ложноотрицательной (ζ) идентификации, учитывающие распространенность С в совокупности идентифицируемых объектов, определяются по формулам:
$\varepsilon = {{P(\bar C) \cdot \alpha } \over {P(\bar C) \cdot \alpha + P(C) \cdot (1 - \beta )}} = {{\alpha \cdot \left( {1 - P(C)} \right)} \over {\alpha \cdot \left( {1 - P(C)} \right) + P(C) \cdot (1 - \beta )}}$;
$\varepsilon = {{P(\bar C) \cdot \alpha } \over {P(\bar C) \cdot \alpha + P(C) \cdot (1 - \beta )}} = {{\alpha \cdot \left( {1 - P(C)} \right)} \over {\alpha \cdot \left( {1 - P(C)} \right) + P(C) \cdot (1 - \beta )}}$;
$\zeta = {{P(C) \cdot \beta } \over {P(C) \cdot \beta + P(\bar C) \cdot (1 - \alpha )}} = {{P(C) \cdot \beta } \over {P(C) \cdot \beta + \left( {1 - P(C)} \right) \cdot (1 - \alpha )}}$.
В свою очередь, модификации показателей прогностической ценности положительного и отрицательного результатов идентификации, учитывающие распространенность С в совокупности идентифицируемых объектов, следует вычислять как $1 - \varepsilon $ и $1 - \zeta $. Множества значений $1 - \varepsilon $ и $1 - \zeta $ на отрезке возможных значений P(C) при фиксированных показателях чувствительности и специфичности будут иметь вид кривых, подобных приведенным на рисунке 4.
Легко доказать, что при равенстве априорных вероятностей идентифицируемого состояния С и противоположного ему состояния $\bar C$ апостериорные вероятности ложноположительной и ложноотрицательной идентификации γ и δ эквивалентны вероятностным ошибкам ε и ζ: $\{ P(C) = P(\bar C)\} \to \{ [\gamma \equiv \varepsilon ] \wedge [\delta \equiv \zeta ]\} $.
Доказанные утверждения имеют важное значение как для судебно-медицинского научного, так и экспертного познания. В рамках первого гносеологического компонента приведенные данные прямо определяют следующий методологический дизайн тестирования достоверности категоричной идентификации:
1) количество объектов с наличием идентифицируемого состояния С должно равняться количеству объектов с отсутствием данного состояния;
2) ошибки идентификации должны быть представлены оценками α, β, γ и δ, а критерии достоверности – оценками 1-α, 1-β, 1-γ и 1-δ;
3) после вычисления оценок γ и δ должны быть разработаны номограммы определения ошибок ε и ζ и соответствующих значений прогностической ценности результатов положительной и отрицательной идентификации 1-ε и 1-ζ для континуума значений P(C) на отрезке при фиксированных значениях 1-α и 1-β.
Для практической судебно-медицинской деятельности доказанные утверждения означают, что формулирование выводов относительно степени достоверности идентификации должно осуществляться с учетом априорной вероятности идентифицируемого состояния P(C) по соответствующим номограммам, подобным приведенной на рисунке 4. В случае отсутствия указанных номограмм в пакете услуг, предоставляемых разработчиком диагностической технологии, первые могут быть созданы самим экспертом, исходя из данных о чувствительности, специфичности и апостериорных ошибках идентификации. Отсутствие информации об указанных оценках, равно как и незнание или недостаточность теоретических предположений относительно распространенности идентифицируемого состояния в совокупности исследуемых объектов является противопоказанием к практическому использованию данной технологии идентификации. Важно подчеркнуть, что большинство диагностических технологий, используемых в судебно-медицинской экспертной практике, предполагают одинаковые вероятности С и $\bar C$ в совокупностях объектов идентификации.
Читать далее раздел "3.4. Интервальное оценивание достоверности судебно-медицинской идентификации"⇒

