Вы здесь
Адаптивный вариант двухэкспоненциальной модели В.А. Куликова для практического применения ее в условиях переменной температуры окружающей среды
Publication in electronic media: 05.07.2011 under http://journal.forens-lit.ru/node/270
Publication in print media: Актуальные вопросы теории и практики судебно-медицинской экспертизы, Красноярск 2007 Вып. 5
A. Ю. Вавилов
г. Ижевск, кафедра судебной медицины ГОУ ВПО «ИГМА Росздрава»
Известно, что наиболее целесообразным для описания температуры трупа, является использование математических моделей, основанных на экспоненциальном характере описываемого процесса [1, 2, 5]. Тем не менее, практическое использование данных моделей несколько затруднено, что объясняется особенностями использованного для их решения математического аппарата.
Так, широко используемые математические модели П. И. Новикова [2] и Е. Ф. Шведа [5], включая в себя ряд коэффициентов, сопровождаются необходимостью ручного, либо полуавтоматического, их подбора [6]. Необходимость этого послужила причиной формирования и развития т.н. «адаптивного подхода» [3,5].
В общем виде, метод адаптивного поиска решения диагностической задачи может быть обозначен как итеративный, то есть, циклический перебор огромного числа значений момента запуска модели процесса охлаждения трупа и значений констант, соответствующих интегральным теплообменным параметрам трупа. Целью итеративного поиска является нахождение того единственного варианта сочетания значений подбираемых параметров, при котором моделируемая температурная кривая максимально точно совпадет с обеими опорными точками (начальной и конечной) реальной выборки процесса.
Очевидно, что при таком подходе точность определения давности смерти, т.е. степень соответствия теоретической кривой посмертной температуры реальным ее значениям, оказывается в прямой зависимости от того, насколько «удачно» оказались подобраны коэффициенты в том или ином конкретном случае.
Более объективным следует считать метод В. А. Куликова [1], который, по сути своей, так же основанный на сопоставлении математической модели реальной выборке процесса, освобождает практического эксперта от необходимости подбора коэффициентов уравнения. Достигается это за счет использования т.н. «термической постоянной времени регулярной стадии охлаждения», для расчета которой автором предложена достаточно простая в практическом применении формула.
Но, следует заметить, что модель Е. Ф. Шведа [5] имеет преимущество, заключающееся в возможности применения ее для условий нестационарной внешней температуры, т.е. при значительных изменениях температуры окружающей среды. Использование при этом модели В. А. Куликова [1], невозможно.
Между тем, существует принципиальная возможность применения указанной выше модели при изменениях внешней температуры.
Соответствующим образом модифицируя выражение [1], мы можем придти к описанию динамики посмертной температуры не единым интервалом давности смерти, а рядом последовательных небольшой продолжительности, что позволяет осуществить «адаптацию» математически прогнозируемого температурного тренда реальным значениям температуры.
«Адаптивный» вариант модели В. А. Куликова [1] реализован посредством следующего двухэкспоненциального выражения:
ФОРМУЛА 1
где Тm0 - внутренняя (прижизненная) температура тела, °С; Тn- температура внешнего слоя (поверхности тела), °С; Тnn - прижизненная температура внешнего слоя, °С; Тc - температура среды, °С; m - время (ДНС), час; А г - продолжительность интервала моделирования, час; m1 - постоянная времени экспоненты регулярной стадии охлаждения; m2 - постоянная времени нерегулярной стадии охлаждения.
Термическая постоянная вычисляется по формуле [1]:
ФОРМУЛА 2
где %\ - термическая постоянная; Ат - интервал между замерами температуры, час; ТхжТ2-значения глубоких температур трупа (°С), разнесенные во времени на At; Tср - температура среды, °С.
Первый член выражения (1) практически идентичен модели [1], с тем отличием, что вместо абсолютных значений давности смерти (т) в уравнении используется понятие интервала моделирования, аналогичное продолжительности отдельных интервалов, на которые разбит посмертный период в модели Е.Ф. Шведа [5].
Второй член выражения (1) описывает динамику поверхностной температуры. В оригинале, В.А. Куликов [1] рекомендует принимать значение Тn (температуры поверхности тела) равным таковому для глубоких его отделов (Тm0).
Между тем известно, что температура поверхностных слоев тела (кожи) практически никогда не равна таковой для глубоких его отделов.
Естественно такое упрощенное представление об охлаждении мертвого тела несколько ухудшает описательные свойства модели [1], снижая ее точность.
Проводя сравнительный анализ предлагаемого «адаптивного» варианта модели, осуществляемый на основании сопоставления ее реальной динамике температуры трупа по методу наименьших квадратов отклонений [4], можем констатировать следующее (Рис. 1).
Как для краниоэнцефальной, так и для температуры печени, «адаптивный» вариант модели обеспечивает хороший уровень предсказания температуры трупа.
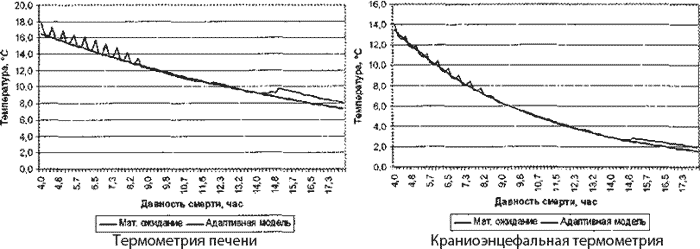
Рис. 1. Температурные тренды «адаптивной» математической модели в соотношении с функцией математического ожидания.
Характеристики соотношения адаптивной математической модели с реальной динамикой охлаждения тел
| Термометрия печени | Краниоэнцефальная термометрия | |
| Дисперсия | 0,186 | 0,031 |
| Корреляция | 0,981 | 0,998 |
Приведенные в таблице 1 значения дисперсии и коэффициента корреляции, подтверждают данный вывод.
При этом следует обратить внимание на низкие показатели дисперсии, характеризующие поведение данной модели при краниоэнцефальной термометрии, что позволяет говорить о предпочтительности использования ее для описания динамики температуры трупа, фиксируемой в полости черепа.
Поскольку в самом начале настоящей статьи, представляя наш «адаптивный» вариант экспоненциальной модели В.А. Куликова [1] ставилась задача практического использования ее при переменных температурах окружающей среды, произведем исследование ее работы в заданных условиях.
Производился мониторинг глубокой температуры трупа на протяжении 20 часов посмертного периода и контроль температуры воздуха, осуществляемые с интервалом в 5 минут.
Измерение температуры производилось в полости черепа, по методике [7]. Скачок температуры моделировался путем быстрого перемещения трупа на каталке из помещения с низкой температурой в помещение с высокой и обратно. При перемещении тела положение самого трупа, а так же его конечностей или одежды не производилось.
Вычисление постоянной времени экспоненты регулярной стадии охлаждения осуществлялось на основании сопоставления ее с выборкой процесса охлаждения участка, следующего за скачком температуры окружающей среды.
Как следует из представленного рисунка, при резком, скачкообразном, изменении температуры окружающей среды, «адаптивная модель» обеспечивает хороший уровень предсказания температуры тела. Максимальная ошибка, отмеченная к концу периода наблюдения (20 часов) составила 1,093°С. Значения дисперсии и коэффициента корреляции между реальными и расчетными значениями температуры трупа составили 0,205 и 0,999 соответственно. Получение таких результатов однозначно свидетельствует о высокой степени соответствия моделируемой температуры трупа ее реальным значениям.
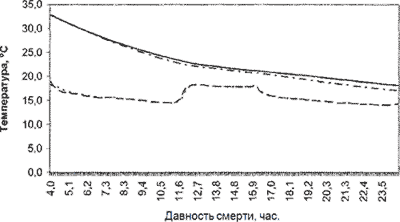
Рис. 2. Поведение адаптивной математической модели при скачкообразных изменениях температуры окружающей среды.
Список литературы:
- Куликов, В.А. Практическая методика измерения ДНС по методу регулярного теплового режима / В.А. Куликов // Современные вопросы судебной медицины и экспертной практики. -Ижевск: Экспертиза. -1998, Вып. Х- С.115 -120.
- Новиков, П.И. Судебно-медицинская диагностика давности наступления смерти способом мо-делирования посмертного процесса изменения температуры трупа: дис. д-ра мед.наук /П.И. Новиков. -М., 1986.-245 с.
- Новиков, П.И. Адаптивные системы в диагностике давности смерти / П.И. Новиков, В.Г. Попов // Судебно-медицинская экспертиза. - 1983. - № 3. - С. 6-9.
- РТМ 44-62. Методика статистической обработки эмпирических данных. - М.: Изд-во комитета стандартов, мер и измер. приборов при СМ СССР, 1966. - 100 с.
- Швед, Е. Ф. Моделирование посмертной термодинамики при установлении давности смерти в условиях меняющейся температуры окружающей среды. Дисс. канд. мед. наук / Е. Ф. Швед -Ижевск, 2006. -144 с.
- Швед, Е. Ф. Методика автоматизированного поиска момента начала процесса постмортального охлаждения (времени смерти) с использованием стандартного табличного процессора - Microsoft Office Excel / Е.Ф. Швед, А.Ю. Вавилов //Проблемы экспертизы в медицине. Научно-практический журнал, 2005. - № 3. Ижевск. «Экспертиза», с. 36-39.
- Щепочкин, О.В. Термометрия головного мозга в аспекте определения давности наступления смерти: дисс... канд. мед. наук/О.В. Щепочкин. -Ижевск., 2001. - 130 с.

